线性代数基础系列（1）——行列式

行列式

1. intro & 概念

• 行列式是一个数，是不同行不同列元素乘积的代数和。

1.1 简单的行列式

• 由二元一次方程组到二阶行列式

为什么要提出行列式？因为我们在解二元一次方程组的时候，会出现两项乘积相减的情况：

$$\begin{array}{l} ax + by = c\\ dx + ey = f \end{array}$$ $$\left\{ \begin{array}{l} x = \frac{ {ce - bf} }{ {ae - bd} }\\ y = \frac{ {af - cd} }{ {ae - bd} } \end{array} \right.$$

提出行列式，可以比较有效率的表示方程组的解。不仅是二元一次方程组，n元一次方程组同样成立。

• 二阶行列式的表示与计算

我们将上面$x、y$的解用行列式表示：

$$\left\{ \begin{matrix} x = \frac{ {\left| {\begin{matrix} c&b\\ f&e \end{matrix} } \right|} }{ {\left| {\begin{matrix} a&b\\ d&e \end{matrix} } \right|} }\\ y = \frac{ {\left| {\begin{matrix} a&c\\ d&f \end{matrix} } \right|} }{ {\left| {\begin{matrix} a&b\\ d&e \end{matrix} } \right|} } \end{matrix} \right.$$

不难发现，二阶行列式的计算很容易：主对角线乘积与副对角线乘积就是二阶行列式的值。

P.S. 主对角线：左上角至右下角，副对角线：左下角至右上角。

• 三阶行列式的计算

  • 对角线法则

  • 对角线法则只能用于二阶、三阶行列式。四阶及以上行列式并不能由三阶的对角线法则直接迁移使用。（敲黑板）

事实上，刚刚二阶行列式的计算用的就是二阶行列式的对角线法则。而三阶行列式的对角线法则比较麻烦。

三阶行列式的表示如下：

$$\left| {\begin{matrix} {a_{11} }&{a_{12} }&{a_{13} }\\ {a_{21} }&{a_{22} }&{a_{23} }\\ {a_{31} }&{a_{32} }&{a_{33} } \end{matrix} } \right|$$

我们使用$D$来表示行列式的值，则$D$可以表示为

$$D = {a_{11} }{a_{22} }{a_{33} } + {a_{12} }{a_{23} }{a_{31} } + {a_{13} }{a_{21} }{a_{32} } - {a_{13} }{a_{22} }{a_{31} } - {a_{12} }{a_{21} }{a_{33} } - {a_{11}{a_{23} }{a_{32} } }$$

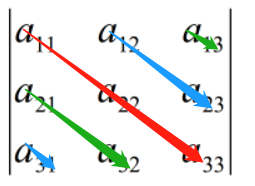
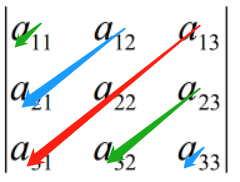
为什么叫对角线法则呢？

图片可以给你最清楚的答案。

但，每一项前的正负号是如何来的呢？高阶的对角线法则如何推导呢？

1.2 排序、逆序、逆序数

• 为了将“对角线法则”推广到n阶行列式，提出以下定义：

• 排序

  • 简单理解，就是一个①不重复的 ②正整数 组成的一维数组。这个数组的长度记为n，则这个排列为n阶排列。

  • 栗子

    • 2 4 1 3 —— 4阶排列
    • 1 3 5 4 2 —— 5阶排列

• 逆序

  • 一个排列中，如果一个大的数排在小的数之前，就称这两个数构成一个逆序。

• 逆序数

  • 排列中的逆序总数成为这个排列的逆序数。

  • 偶排列与奇排列

    • 若逆序数是偶数，就是偶排列。否则是奇排列。
    • 排列中，偶排列对应正号，奇排列对应符号。

  • 栗子

    • 2 4 3 1 —— 1 + 3 = 4 ，逆序数为4，偶排列
    • 3 1 5 4 2 —— 1 + 1 + 3 = 5 ，逆序数为5，奇排列

  • 求逆序数伪代码（便于理解）

    for i=1 to num.len:
      for j=0 to i-1:
          if num[j] > num[i]:
              inver_num ++
    

  • 自然排列

    • 只包括自然数，且以公差为1单调递增。
    • 栗子
      • 1 2 3 4

1.3 n阶行列式

• $n$阶行列式等于所有取自不同行不同列的n个元素的乘积的代数和，逆序数为偶数时带正号，逆序数为奇数时带负号，共有$n!$项。

  • 为什么项数是$n!$，下面给出说明。

    三阶行列式中，共有6项。首先确定自然排序是按行或是列。假设按行自然排序的通项是${a_{1x_{1} } }{a_{2x_{2} } }{a_{3x_{3} } }$，则接下来的工作就是选定$x_{1}、x_{2}、x_{3}$的值。共有$C_3^1C_2^1C_1^1$种情况，所以就是$3!$。其他阶行列式同理。

• 计算

  • 使用三阶行列式来说明计算过程，并顺便验证对角线法则。

    假设按行自然排序通项是${a_{1x_{1} } }{a_{2x_{2} } }{a_{3x_{3} } }$，则所有的可能为

    $${a_{11} }{a_{22} }{a_{33} } 、 {a_{12} }{a_{23} }{a_{31} } 、 {a_{13} }{a_{21} }{a_{32} } 、 {a_{13} }{a_{22} }{a_{31} } 、 {a_{12} }{a_{21} }{a_{33} } 、 {a_{11}{a_{23} }{a_{32} } }$$

    根据逆序数，我们可以确定它们每一项的符号:

项	逆序数	符号
${a_{11} }{a_{22} }{a_{33} }$	0	+
${a_{11} }{a_{23} }{a_{32} }$	1	-
${a_{12} }{a_{21} }{a_{33} }$	1	-
${a_{12} }{a_{23} }{a_{31} }$	2	+
${a_{13} }{a_{21} }{a_{32} }$	2	+
${a_{13} }{a_{22} }{a_{31} }$	3	-

• 对角线规则计算出的结果是：

$$D = {a_{11} }{a_{22} }{a_{33} } + {a_{12} }{a_{23} }{a_{31} } + {a_{13} }{a_{21} }{a_{32} } - {a_{13} }{a_{22} }{a_{31} } - {a_{12} }{a_{21} }{a_{33} } - {a_{11}{a_{23} }{a_{32} } }$$

可以看到，是吻合的。

综上，总结计算行列式的方法：先写出行/列的通项，再写出所有项，利用逆序数计算出每一项的符号，最后累加就是行列式的值。但我们一般不会用这个方法。

2. 性质

目的：简化计算量

性质1. 转置后，行列式的值不变

• 因为这个性质，所以下面只讨论行。行与列是等价的。

性质2. 某行（列）有公因数k，可以把k提出来

• 推论：若某一行（列）元素都为0，则$D=0$
• tips：公因数法：若其他行（列）相加到特定行（列）后，这行（列）所有元素值相等，则可以构造出都是1元素的行（列），之后用于构造0 。

性质3. 对换行列式中两行（列）的位置，行列式变号

• 推论：两行（列）相同或成比例，$D=0$

性质4. 某行所有元素都是两个数的和，则可把行列式写成两个行列式之和。

• 推论：n阶行列式如果每一行都是两个数的和，则应写成${2^n}$个$n$阶行列式的和

• 证明：每一行有两个部分，两两组合共有${2^n}$种可能性。

*性质5. 某行的k倍加到另一行，行列式的值不变。

3. 展开公式（高频考点）

3.1 余子式

• 去掉第$i$行第$j$列，剩余的行列式称为余子式${M_{ij} }$，是$n-1$阶的行列式。
• 目的：降维

3.2 代数余子式

• 代数余子式使用${A_{ij} }$表示，${A_{ij} } = {( - 1)^{i + j} }*{M_{ij} }$

  • 推论：${A_{ij} }$与${a_{ij} }$的数值大小无关

3.3 展开公式

• intro：由对角线法则引入代数余子式的展开计算。

$$\begin{array}{l} D = {a_{11} }{a_{22} }{a_{33} } + {a_{12} }{a_{23} }{a_{31} } + {a_{13} }{a_{21} }{a_{32} } - {a_{13} }{a_{22} }{a_{31} } - {a_{12} }{a_{21} }{a_{33} } - {a_{23} }{a_{32} }{a_{11} }\\ = {a_{11} }({a_{22} }{a_{33} } - {a_{23} }{a_{32} }) - {a_{12} }({a_{21} }{a_{33} } - {a_{23} }{a_{31} }) + {a_{13} }({a_{21} }{a_{32} } - {a_{22} }{a_{31} })\\ = {a_{11} }{A_{11} } + {a_{12} }{A_{12} } + {a_{13} }{A_{13} } \end{array}$$

这样，我们就把对角线法则产生的结果用代数余子式给表示出来了。这就是按第一行展开的结果。

这样计算的好处是更容易。因为余子式是降维的操作，可以通过不断的降维，最后达到二阶行列式，从而简化计算。

• $n$阶行列式：是它的任意一行（列）的所有元素与它代数余子式的乘积之和。

按行展开公式：

$$D = \sum\limits_{j = 1}^n { {a_{ij} }{A_{ij} } }$$

按列展开公式：

$$D = \sum\limits_{i = 1}^n { {a_{ij} }{A_{ij} } }$$

• tips：选0比较多的行（列）进行展开，减小计算量。

• 定理：行列式某一行（列）所有元素与另一行（列）相应元素的代数余子式乘积之和等于0

3.4 拉普拉斯行列式

• 主对角线形式

$$\left| {\begin{matrix} A&0\\ *&B \end{matrix} } \right| = \left| {\begin{matrix} A&*\\ 0&B \end{matrix} } \right| = \left| A \right|\left| B \right|$$

• 副对角线形式

$$\left| {\begin{matrix} 0&A\\ B&* \end{matrix} } \right| = \left| {\begin{matrix} *&A\\ B&0 \end{matrix} } \right| = {( - 1)^{mn} }\left| A \right|\left| B \right|$$

此处，$m、n$分别是行列式$A、B$的行或列的长度。

• tips：存在比较多的0，可以采用交换行列，构造拉普拉斯行列式。

3.5 范德蒙德行列式

$$\left| {\begin{matrix} 1&1&1&1\\ {a_1^{} }&{a_2^{} }&{a_3^{} }&{a_4^{} }\\ {a_1^2}&{a_2^2}&{a_3^2}&{a_4^2}\\ {a_1^3}&{a_2^3}&{a_3^3}&{a_3^3} \end{matrix} } \right| = \prod\limits_{1 \le j \le i \le n}^{} {({a_i} - {a_j})}$$

公式可能比较晦涩难懂，举个栗子

$$\left| {\begin{matrix} 1&1&1\\ 1&2&3\\ 1&4&9 \end{matrix} } \right|$$

它的答案是：

$$(2 - 1)*(3 - 1)*(3 - 2) = 2$$

• tips：存在规律的次方关系，构造范德蒙德。

3.6 爪形行列式

$$\left| {\begin{matrix} { {a_{11} } }&{ {a_{12} } }&{ {a_{13} } }&{ {a_{14} } }\\ { {a_{21} } }&{ {a_{22} } }&0&0\\ { {a_{31} } }&0&{ {a_{33} } }&0\\ { {a_{41} } }&0&0&{ {a_{44} } } \end{matrix} } \right|$$

是不是很形象，和爪子一模一样。
除了标注是0的元素，其余元素都不为0，这样的行列式称为爪形行列式。

有什么用处呢，可以利用主对角线上的属性，把第一行或者第一列消除，这样就变成了三角行列式，计算超级快呀。

3.7 特征值求解问题

• 求解步骤

  • 先不看主对角线，观察其他6个数，某两行（列）相加后，是否能产生0的同时，又能产生关于λ的公因式（待续）

3.8 三角行列式

• 右上三角行列式、左下三角行列式

$$D = \prod\limits_{i = 1}^n { {a_{ii} } }$$

D = 主对角线元素乘积

• 左上三角行列式、右下三角行列式

$$D = {( - 1)^{\frac{1}{2}n(n - 1)} }{a_{1,n} }{a_{2,n - 1} } \cdots {a_{n - 1,2} }{a_{n,1} }$$

D = 副对角线元素乘积*符号

4. 克拉默法则

• 给定n个方程，n个未知数的方程组，若$D≠0$，则方程组有唯一解。

方程组：

$$\begin{matrix} {a_{11} }{x_1} + {a_{12} }{x_2} + \cdots {a_{1n} }{x_n} = {b_1}\\ {a_{21} }{x_1} + {a_{22} }{x_2} + \cdots {a_{2n} }{x_n} = {b_2}\\ \vdots \\ {a_{n1} }{x_1} + {a_{n2} }{x_2} + \cdots {a_{nn} }{x_n} = {b_n} \end{matrix}$$

解的形式：

$${x_i} = \frac{ { {D_i} } }{D}$$

其中，

$${D_i} = \left| {\begin{matrix} {\begin{matrix} { {a_{11} } }&{ \cdots {a_{1,i - 1} } }&{ {b_1} }\\ { {a_{21} } }&{ \cdots {a_{2,i - 1} } }&{ {b_2} }\\ { {a_{31} } }&{ \cdots {a_{3,i - 1} } }&{ {b_3} } \end{matrix} }&{\begin{matrix} { {a_{1,i + 1} } }& \cdots &{ {a_{1n} } }\\ { {a_{2,i + 1} } }& \cdots &{ {a_{2n} } }\\ { {a_{3,i + 1} } }& \cdots &{ {a_{3n} } } \end{matrix} }\\ {\begin{matrix} { {a_{41} } }&{ \cdots {a_{4,i - 1} } }&{ {b_4} }\\ \vdots & \vdots & \vdots \\ { {a_{n1} } }&{ \cdots {a_{n,i - 1} } }&{ {b_n} } \end{matrix} }&{\begin{matrix} { {a_{4,i + 1} } }& \cdots &{ {a_{4n} } }\\ \vdots & \cdots &{ {a_{5n} } }\\ { {a_{1,i + 1} } }& \cdots &{ {a_{6n} } } \end{matrix} } \end{matrix} } \right|$$

写的这么玄乎，其实就是把常数项那一列替换到$X_{i}$的行列式$Di$的第$i$列。

$$D = \left| {\begin{matrix} { {a_{11} } }& \cdots &{ {a_{1n} } }\\ \vdots & \cdots & \vdots \\ { {a_{n1} } }& \cdots &{ {a_{nn} } } \end{matrix} } \right|$$

推论

推论1：若齐次方程组的系数行列式不为0，则方程组有且只有一组零解。
简单说明：$D≠0$，说明有唯一解。而齐次方程组本身就一定有一个零解。所以说 $D≠0$可以唯一确定齐次方程组只有零解。

推论2：若齐次方程组有非零解，则它的系数行列式必为0 （推论1的逆否命题）

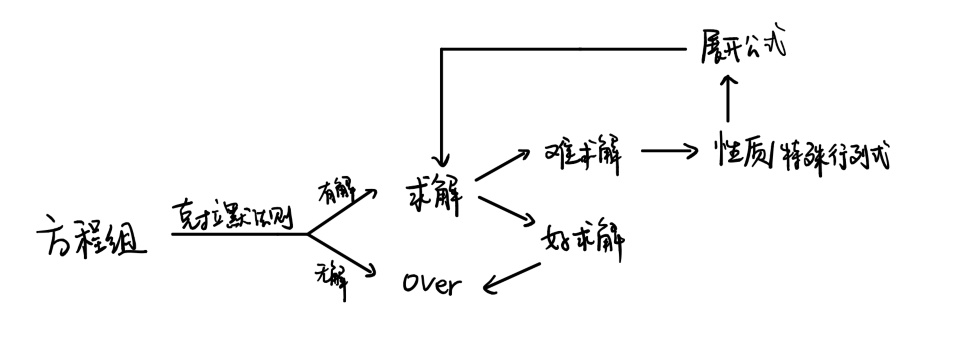
5. 总结

其实这章说了这么多，都是为了解方程组。

以上，就是我对第一章行列式的总结。谢谢观看~