线性代数基础系列（2）——矩阵

矩阵

今天复习了第二章矩阵。老实说，内容很多也很杂，需要花时间好好吸收。

1. intro&概念

1.1 什么是矩阵

• 首先，什么是矩阵呢？

度娘给出的解释是这样的：在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合，最早来自于方程组的系数及常数所构成的方阵。
概念比较….抽象。都说是看脸的时代（doge），那就直接给出它的数学符号表达：

$$\left[ {\begin{matrix} {\begin{matrix} 1&2 \end{matrix} }\\ {\begin{matrix} 3&4 \end{matrix} }\\ {\begin{matrix} 5&6 \end{matrix} } \end{matrix} } \right]$$

这就是一个$3*2$的矩阵。代表着有三行、两列个数。

• 为什么要引出矩阵概念呢？

上一章中，我们引出行列式的目的是为了计算线性方程组。通过克莱姆法则，我们可以计算出这个线性方程组的解。但前人们热衷于探（tou）究（lan），想要更有效率的计算出线性方程组，所以提出矩阵的概念，用矩阵去表示线性方程组。

• 方阵

如果矩阵的行列数相等，我们称之方阵。

• 同型矩阵

如果两个矩阵的行数相等，列数也相等，则我们称之为同型矩阵。

• 矩阵相等

如果两个矩阵是同型矩阵，且对应位置元素值全都相等，则我们称之为矩阵相等。

1.2 矩阵类型

• 零矩阵$0$

一个矩阵所有元素都是0。

$$\left[ {\begin{matrix} 0&0&0\\ 0&0&0\\ 0&0&0 \end{matrix} } \right]$$

• 对角矩阵

除了主对角线上的元素不为0，其他位置上的元素都为0。

$$\left[ {\begin{matrix} { {a_{11} } }&0&0\\ 0&{ {a_{22} } }&0\\ 0&0&{ {a_{33} } } \end{matrix} } \right]$$

• 单位矩阵$E$

一个对角矩阵中，主对角线上元素值都为1。

$$\left[ {\begin{matrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{matrix} } \right]$$

• 上三角矩阵

主对角线下元素值都为0

$$\left[ {\begin{matrix} { {a_{11} } }&{ {a_{12} } }&{ {a_{13} } }\\ 0&{ {a_{22} } }&{ {a_{23} } }\\ 0&0&{ {a_{33} } } \end{matrix} } \right]$$

用数学语言来说，$i>j$时，$a_{ij}=0$。（证明题用）

• 下三角矩阵

主对角线上元素都为0

$$\left[ {\begin{matrix} { {a_{11} } }&0&0\\ { {a_{21} } }&{ {a_{22} } }&0\\ { {a_{31} } }&{ {a_{32} } }&{ {a_{33} } } \end{matrix} } \right]$$

用数学语言来说，$i<j$时，$a_{ij}=0$。（证明题用）

2. 运算

2.1 加法

• 计算前提：同型矩阵

• 计算规则：对应位置相加

$$\left[ {\begin{matrix} { {a_{11} } }&{ {a_{12} } }&{ {a_{13} } }\\ { {a_{21} } }&{ {a_{22} } }&{ {a_{23} } }\\ { {a_{31} } }&{ {a_{32} } }&{ {a_{33} } } \end{matrix} } \right] + \left[ {\begin{matrix} { {b_{11} } }&{ {b_{12} } }&{ {b_{13} } }\\ { {b_{21} } }&{ {b_{22} } }&{ {b_{23} } }\\ { {b_{31} } }&{ {b_{32} } }&{ {b_{33} } } \end{matrix} } \right] = \left[ {\begin{matrix} { {a_{11} } + {b_{11} } }&{ {a_{12} } + {b_{12} } }&{ {a_{13} } + {b_{13} } }\\ { {a_{21} } + {b_{21} } }&{ {a_{22} } + {b_{22} } }&{ {a_{23} } + {b_{23} } }\\ { {a_{31} } + {b_{31} } }&{ {a_{32} } + {b_{32} } }&{ {a_{33} } + {b_{33} } } \end{matrix} } \right]$$

• 符合规律：

  • 具有交换律

    $$A+B=B+A$$

  • 结合律

    $$(A+B)+C=A+(B+C)$$

2.2 矩阵数乘

• 计算规则：每个元素值对应缩放k倍

$$k\left[ {\begin{matrix} { {a_{11} } }&{ {a_{12} } }&{ {a_{13} } }\\ { {a_{21} } }&{ {a_{22} } }&{ {a_{23} } }\\ { {a_{31} } }&{ {a_{32} } }&{ {a_{33} } } \end{matrix} } \right] = \left[ {\begin{matrix} {k{a_{11} } }&{k{a_{12} } }&{k{a_{13} } }\\ {k{a_{21} } }&{k{a_{22} } }&{k{a_{23} } }\\ {k{a_{31} } }&{k{a_{32} } }&{k{a_{33} } } \end{matrix} } \right]$$

• 符合规律：

  • 具有交换律

    $$kAB=AkB$$

  • 结合律

    $$(kA)B=k(AB)$$

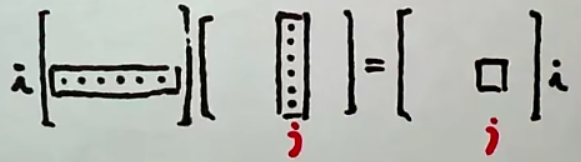
2.3 矩阵乘法（敲黑板！敲坏黑板！）

• 计算前提：假设$A$是$m*n$的矩阵，B是$p*q$的矩阵，则当$n=p$，才可以进行$AB$矩阵乘法运算。

• 计算规则：

$$AB = C$$ $$\left[ {\begin{matrix} { {a_{11} } }&{ {a_{12} } }&{ {a_{13} } }\\ { {a_{21} } }&{ {a_{22} } }&{ {a_{23} } }\\ { {a_{31} } }&{ {a_{32} } }&{ {a_{33} } } \end{matrix} } \right]\left[ {\begin{matrix} { {b_{11} } }&{ {b_{12} } }&{ {b_{13} } }\\ { {b_{21} } }&{ {b_{22} } }&{ {b_{23} } }\\ { {b_{31} } }&{ {b_{32} } }&{ {b_{33} } } \end{matrix} } \right] = \left[ {\begin{matrix} { {c_{11} } }&{ {c_{12} } }&{ {c_{13} } }\\ { {c_{21} } }&{ {c_{22} } }&{ {c_{23} } }\\ { {c_{31} } }&{ {c_{32} } }&{ {c_{33} } } \end{matrix} } \right]$$

其中，

$$A.size=m*s,B.size=s*n$$ $${c_{ij} } = \sum\limits_{k = 1}^s { {a_{ik} }{b_{kj} } }$$

公式比较丑…用一张图形象的解释一下：

计算过程就是左边A矩阵对应第i行，右边B矩阵对应第j列，对s个元素分别对应位置做相乘，累加和就是$cij$的值。

• 计算步骤：
  • 0.不要心急
  • 1.确定是否能进行矩阵乘法
  • 2.左矩阵的每一行乘右矩阵的每一列，加在一起，填到结果对应位置
  • 3.验算
• 符合规律
• 1.结合律 $$(AB)C=A(BC)$$
• 2.分配律 $$A(B+C)=AB+AC$$ $$(B+C)A=BA+CA$$
• 3.恒等变形 $$A=AE=EA$$

• 4.方阵符合的规律

  $$AA=A^2$$ $$AA...A=A^k$$

• 注意点：

  • 1.$AB≠BA$

    即不满足交换律。其实很容易理解，因为计算规则是左边行乘右边列，交换必然导致结果改变。

  • 2.$AB=0$推不出$A=0$或$B=0$

    因为导致AB=0不是因为A=0或B=0，而是A中元素与B中元素一起决定的，最后累加和才等于0。

  • 3.由$AB=AC$且$A≠0$推不出$B=C$

    如果A存在逆，可以推出B=C。但A不存在逆的情况下，推不出B=C。

• 常见公式：

  • 1.平方和

    $$(A+B)^2=A^2+AB+BA+B^2$$ $$(A+E)^2=A^2+2A+E$$

  • 2.平方差

    $$(A+B)(A-B)=A^2-AB+BA-B^2$$ $$(A+E)(A-E)=(A-E)(A+E)=A^2-E$$

• 方程组与矩阵乘法:

$$\begin{matrix} {a_{11} }{x_1} + {a_{12} }{x_2} + \cdots {a_{1n} }{x_n} = {b_1}\\ {a_{21} }{x_1} + {a_{22} }{x_2} + \cdots {a_{2n} }{x_n} = {b_2}\\ \vdots \\ {a_{n1} }{x_1} + {a_{n2} }{x_2} + \cdots {a_{nn} }{x_n} = {b_n} \end{matrix}$$

我们使用系数矩阵$A$、未知数矩阵$x$、常数项矩阵$b$来描述这个方程组。

$$A = \left[ {\begin{matrix} { {a_{11} } }& \cdots &{ {a_{1n} } }\\ \vdots & \cdots & \vdots \\ { {a_{n1} } }& \cdots &{ {a_{nn} } } \end{matrix} } \right]$$ $$x = {\left[ {\begin{matrix} { {x_1} }& \cdots &{ {x_n} } \end{matrix} } \right]^T}$$ $$b = {\left[ {\begin{matrix} { {b_1} }& \cdots &{ {b_n} } \end{matrix} } \right]^T}$$

这个方程组可以写作$Ax=b$，为第三章埋下伏笔啦~

2.4 转置

转置其实很简单。本来元素是对号入座的，$a_{ij}$就应该坐在$a_{ij}$的位置，但转置把这个位置换了一下，$a_{ij}$坐在了$a_{ji}$位置上。

从某个矩阵来观察这个现象可能会更直观一些。

$$A = \left[ {\begin{matrix} {\begin{matrix} { {a_{11} } }&{ {a_{12} } }&{ {a_{13} } } \end{matrix} }\\ {\begin{matrix} { {a_{21} } }&{ {a_{22} } }&{ {a_{23} } } \end{matrix} } \end{matrix} } \right]$$ $${A^T} = \left[ {\begin{matrix} {\begin{matrix} { {a_{11} } }\\ { {a_{12} } }\\ { {a_{13} } } \end{matrix} }&{\begin{matrix} { {a_{21} } }\\ { {a_{22} } }\\ { {a_{23} } } \end{matrix} } \end{matrix} } \right]$$

2.4.1 运算法则

• 1.加法转置 $$(A+B)^T=A^T+B^T$$
• 2.常数转置 $$(kA)^T=k(A)^T$$
• 3.*结合转置 $$(AB)^T=B^TA^T$$
• 4.自我转置 $$(A^T)^T=A$$

2.4.2 特殊矩阵

• 1.对称矩阵

若$A^T=A$，则$A$为对称矩阵。换一个等价的说法，对任意$i,j$，都有$a_{ij}=a_{ji}$，则这个矩阵是对称矩阵。

• 2.反对称矩阵

若$A^T=-A$，则$A$为对称矩阵。换一个等价的说法，对任意$i,j$，都有$a_{ij}=-a_{ji}$，则这个矩阵是对称矩阵。

• 3.列向量

定义：$\alpha 和 \beta$是n维列向量。
有如下6个矩阵相乘结果：

$$\alpha\beta^T、\beta\alpha^T、\alpha\alpha^T$$ $$\beta^T\alpha、\alpha^T\beta、\alpha^T\alpha$$

• 遇到向量相乘的问题时，
  • 问自己：结果是矩阵还是数
  • 上面三个：都是矩阵，列向量乘行向量。结果矩阵任意两行（列）成比例，二阶行列式为0，秩为1。
  • 下面三个：都是数行向量乘列向量。结果矩阵的迹对应下面结果矩阵的值。

设

$$\alpha = \left[ {\begin{matrix}1\\3\\{ - 2}\end{matrix} } \right]$$

• 推论：$AA^T$一定是对称矩阵

$$\alpha {\alpha ^T} = \left[ {\begin{matrix}1&3&{ - 2}\\3&9&{ - 6}\\{ - 2}&{ - 6}&4\end{matrix} } \right]$$

• 推论：$A^TA$是平方和，一定大于等于0，且值为$AA^T$的迹。 $${\alpha ^T}\alpha = 1*1 + 3*3 + ( - 2)*( - 2) = 14=1+9+4$$

tips：遇到行在前面，列在后面，要知道它是个数，可以乘完提到外面

• 4.对角矩阵

两个矩阵都是对角矩阵，乘完一定还是对角矩阵，满足交换律

$$\left[ {\begin{matrix} { {a_{11} } }&{}&{}\\ {}&{ {a_{22} } }&{}\\ {}&{}&{ {a_{33} } } \end{matrix} } \right]\left[ {\begin{matrix} { {b_{11} } }&{}&{}\\ {}&{ {b_{22} } }&{}\\ {}&{}&{ {b_{33} } } \end{matrix} } \right] = \left[ {\begin{matrix} { {a_{11} }{b_{11} } }&{}&{}\\ {}&{ {a_{22} }{b_{22} } }&{}\\ {}&{}&{ {a_{33} }{b_{33} } } \end{matrix} } \right]$$

• 推论：

  $${\left[ {\begin{matrix} { {a_{11} } }&{}&{}\\ {}&{ {a_{22} } }&{}\\ {}&{}&{ {a_{33} } } \end{matrix} } \right]^n} = \left[ {\begin{matrix} { {a_{11} }^n}&{}&{}\\ {}&{ {a_{22} }^n}&{}\\ {}&{}&{ {a_{33} }^n} \end{matrix} } \right]$$

• 推论：

  $${\left[ {\begin{matrix} { {a_{11} } }&{}&{}\\ {}&{ {a_{22} } }&{}\\ {}&{}&{ {a_{33} } } \end{matrix} } \right]^{ - 1} } = \left[ {\begin{matrix} { {a_{11} }^{ - 1} }&{}&{}\\ {}&{ {a_{22} }^{ - 1} }&{}\\ {}&{}&{ {a_{33} }^n} \end{matrix} } \right]$$

3. 伴随矩阵、可逆矩阵

3.1 伴随矩阵

• 定义

既然叫伴随矩阵，那肯定是给人家当绿叶用的。伴随矩阵是用于求逆矩阵其中的一个步骤，所以叫做伴随。

它真正的定义是：$A$是一个$n$阶矩阵，行列式$|A|$所有的代数余子式构成如下矩阵：

$${A^*}{\rm{ = } }\left[ {\begin{matrix} { {A_{11} } }& \cdots &{ {A_{1n} } }\\ \vdots & \cdots & \vdots \\ { {A_{n1} } }& \cdots &{ {A_{nn} } } \end{matrix} } \right]$$

• 定理

这个定理非常重要！也比较容易证明~

$$A{A^*} = {A^*}A = \left| A \right|E$$

• 其他公式

1. $${(kA)^*} = {k^{n - 1} }{A^*}$$
2. $${({A^*})^T} = {({A^T})^*}$$
3. $$\left| { {A^*} } \right| = {\left| A \right|^{n - 1} }$$
4. $${({A^*})^*} = {\left| A \right|^{n - 2} }A$$
5. $${({A^*})^{ - 1} } = {({A^{ - 1} })^*} = \frac{1}{ {\left| A \right|} }A$$
6. $$r({A^*}) = \left\{ {\begin{matrix} {n \qquad r(A) = n}\\ {1 \qquad r(A) = n - 1}\\ {0 \qquad r(A) < n - 1} \end{matrix} } \right.$$

• 伴随矩阵的求解方法

1.根据上面的定理进行变形就可以求解（定义法）。

$${A^*} = \left| A \right|{A^{ - 1} }$$

2.二阶伴随矩阵—口算法（常用）
主对角线互换位置，副对角线改为相反数。

$${\left[ {\begin{matrix} a&b\\ c&d \end{matrix} } \right]^*} = \left[ {\begin{matrix} d&{ - b}\\ { - c}&a \end{matrix} } \right]$$

3.2 可逆矩阵

• 定义

A是n阶矩阵，如果存在n阶矩阵B，使得$AB=BA=E$成立，则$A$是可逆矩阵，B是A的逆矩阵，记作$A^{-1}=B$。

P.S. 成立条件：A、B都要是方阵，且矩阵乘法结果是单位矩阵，两个条件缺一不可。

但实际上，后面我们都用推论1。因为定义太复杂，可以简化。

• 命题1（更进一步）

如果矩阵A是可逆的，那么A的逆矩阵是唯一的，记作$A^{-1}$。

简单证明：
设$B,C$都是$A$的逆矩阵，即$AB=BA=E,AC=CA=E$

$$B=BE=B(AC)=(BA)C=EC=C$$

即逆矩阵是唯一的。
证明过程并不重要，但恒等变形法很重要。即$B=BE$这一步，需要好好掌握这个思想。

• 推论1（更进一步）

由定义与命题1，我们可以将定义简化：

A,B是n阶矩阵，若$AB=E$，则$A^{-1}=B$。

所以，只需要证明AB=E，就能得出A的逆矩阵是B了。

• 定理1

A方阵可逆的充要条件是$\left| A \right| \ne 0$。

tips：所以，在计算矩阵的逆之前，应先计算是否可逆。

• 定理2

设A、B矩阵均为n阶方阵。若$AB=E$，则$BA=E$。

即计算出$AB=E$可以推出A的逆矩阵是B，B的逆矩阵是A。

• 性质

1.如果$A$可逆，则$(A^{-1})^{-1}=A$

2.如果$A$可逆，且$k \ne 0$，则$kA$可逆，${(kA)^{ - 1} } = \frac{1}{k}{A^{ - 1} }$

3.如果$A,B$均可逆，则$AB$也可逆，且${(AB)^{ - 1} } = {B^{ - 1} }{A^{ - 1} }$

4.如果$A$可逆，则$A^T$也可逆，且${({A^T})^{ - 1} } = {({A^{ - 1} })^T}$

5.如果$A$可逆，有$\left| { {A^{ - 1} } } \right| = \frac{1}{ {\left| A \right|} }$

• 逆矩阵的求解

经过定理1，确定矩阵存在逆后，就可以对矩阵进行求解了。

1.公式法

在伴随矩阵中，我们给出这个式子：

$$A{A^*} = {A^*}A = \left| A \right|E$$

两边同除以$\left| A \right|$，

$$A\frac{ { {A^*} } }{ {\left| A \right|} } = \frac{ { {A^*} } }{ {\left| A \right|} }A = E$$

我们可以看到，$\frac{ { {A^*} } }{ {\left| A \right|} }$就是$A$的逆矩阵了。

2.定义法

由公式$AB=E$，凑出$A、B$的形式即可。

常用的有待定系数法（自己整出来的）：

用一道例题来说明：

A是n阶矩阵，满足$A^2-3A-2E=0$，则$A^{-1}?(A+E)^{-1}?$
首先，A对应的就是A的位置，A的逆对应的就是B的位置。所以，我们现在要确定B。$A(A-3E)-2E=A^2-3A-2E$，整理得A(A-3E)=2E，最后得到$A\frac{1}{2}(A - 3E) = E$，所以$B=A^{-1}=\frac{1}{2}(A - 3E)$。
同理，$(A+E)^{-1}$在这里作为A，B需要自己确定。设$(A+E)(A+xE)=A^2+(1+x)A+xE$，得x=-4。注意，计算出x=-4这一步只需要看A的系数。接下来将-4带回，我们设的式子变为$(A+E)(A+xE)=A^2-3A-4E$这个式子，再进行变形就可以转换回原式，即$原式=A^2-3A-4E+2E=0$。则有$A^2-3A-4E=-2E$，最终，$(A+E)(A-4E)=-2E$，同除-2，结果就出来了。最后结果是$- \frac{1}{2}(A - 4E)$

转圈法

下面有一道转圈法例题，其实本质很简单，就是将最左的矩阵消去，再添进最右边。最右的矩阵同理。

• 初等行变换

见下一章。

• 分块

1.主对角线分块

$${\left[ {\begin{matrix} A&0\\ 0&B \end{matrix} } \right]^{ - 1} } = \left[ {\begin{matrix} { {A^{ - 1} } }&0\\ 0&{ {B^{ - 1} } } \end{matrix} } \right]$$

2.副对角线分块

记得更换顺序！！

$${\left[ {\begin{matrix} 0&A\\ B&0 \end{matrix} } \right]^{ - 1} } = \left[ {\begin{matrix} 0&{ {B^{ - 1} } }\\ { {A^{ - 1} } }&0 \end{matrix} } \right]$$

• 注意点

1.加法参与运算很少。当A,B,A+B都可逆时，一般${(A + B)^{ - 1} } \ne {A^{ - 1} } + {B^{ - 1} }$

4.分块矩阵

• 定义

分块矩阵是一个矩阵，它是把矩阵分别按照横竖分割成一些小的子矩阵。然后把每个小矩阵看成一个元素。（取自度娘）

简单来说，就是分治啦~变成小的矩阵，可以利用现成的结论更快解决，何乐而不为？

• 原则：按需切块

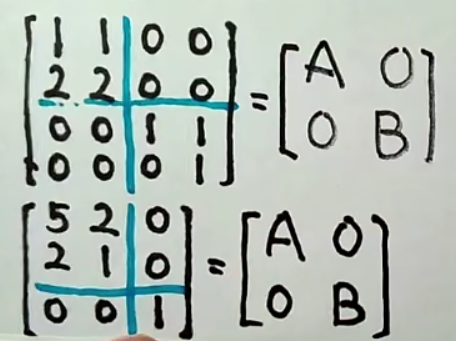
• 运算法则

1.

$$\left[ {\begin{matrix} { {A_1} }&{ {A_2} }\\ { {A_3} }&{ {A_4} } \end{matrix} } \right] + \left[ {\begin{matrix} { {B_1} }&{ {B_2} }\\ { {B_3} }&{ {B_4} } \end{matrix} } \right] = \left[ {\begin{matrix} { {A_1} + {B_1} }&{ {A_2} + {B_2} }\\ { {A_3} + {B_3} }&{ {A_4} + {B_4} } \end{matrix} } \right]$$

2.

$$\left[ {\begin{matrix} { {A_1} }&{ {A_2} }\\ { {A_3} }&{ {A_4} } \end{matrix} } \right]\left[ {\begin{matrix} { {B_1} }&{ {B_2} }\\ { {B_3} }&{ {B_4} } \end{matrix} } \right] = \left[ {\begin{matrix} { {A_1}{B_1} + {A_2}{B_3} }&{ {A_1}{B_2} + {A_2}{B_4} }\\ { {A_3}{B_1} + {A_4}{B_3} }&{ {A_3}{B_2} + {A_4}{B_4} } \end{matrix} } \right]$$

3.

$${\left[ {\begin{matrix} { {A_1} }&{ {A_2} }\\ { {A_3} }&{ {A_4} } \end{matrix} } \right]^T} = \left[ {\begin{matrix} {A_1^T}&{A_3^T}\\ {A_2^T}&{A_4^T} \end{matrix} } \right]$$

4.

$${\left[ {\begin{matrix} { {A_1} }&0\\ 0&{ {A_4} } \end{matrix} } \right]^n} = \left[ {\begin{matrix} {A_1^n}&0\\ 0&{A_4^n} \end{matrix} } \right]$$

5.

$${\left[ {\begin{matrix} { {A_1} }&0\\ 0&{ {A_4} } \end{matrix} } \right]^{ - 1} } = \left[ {\begin{matrix} {A_1^{ - 1} }&0\\ 0&{A_4^{ - 1} } \end{matrix} } \right]$$

6.
记得换顺序！

$${\left[ {\begin{matrix} 0&{ {A_2} }\\ { {A_3} }&0 \end{matrix} } \right]^{ - 1} } = \left[ {\begin{matrix} 0&{A_3^{ - 1} }\\ {A_2^{ - 1} }&0 \end{matrix} } \right]$$

7.按列分块

方阵的行列式

• 定义

设A是n阶矩阵，则其所有元素所构成的行列式就是方阵A的行列式，记作${\left| A \right|}$:

$$\left| A \right|{\rm{ = } }\left| {\begin{matrix} { {a_{11} } }& \cdots &{ {a_{1n} } }\\ \vdots & \cdots & \vdots \\ { {a_{n1} } }& \cdots &{ {a_{nn} } } \end{matrix} } \right|$$

• 注意点

1. 方阵才有行列式
2. 记得$A=0$与${\left| A \right|}=0$不要混淆

• 公式

1. $\left| { {A^T} } \right| = \left| A \right|$
2. $\left| {kA} \right| = {k^n}\left| A \right|$
   因为有n行，所以是n次方。
3. 最重要的公式！行列式乘法公式 $$\left| A \right|\left| B \right| = \left| {AB} \right|$$ 特别地， $$\left| { {A^2} } \right| = {\left| A \right|^2}$$
4. $$\left| { {A^*} } \right| = {\left| A \right|^{n - 1} }$$
5. $$\left| { {A^{ - 1} } } \right| = \frac{1}{ {\left| A \right|} }$$
6. 拉普拉斯行列式