线性代数基础系列（3）——矩阵与线性方程组

矩阵与线性方程组

很快啊（doge），马上到第三章了。第二章我们介绍了矩阵这一个新定义的算子，现在我们要把这个算子投入运用———即解线性方程组中。在解之前呢，需要补充一些前置知识，例如高斯消元法、矩阵的秩等等，综合这些知识，我们就又新点了一个技能点了。

1.高斯消元法

高斯消元法….其实大家小学就学过了，就是解二元一次方程组时用的消元法~现在简单帮大家回忆一下= =

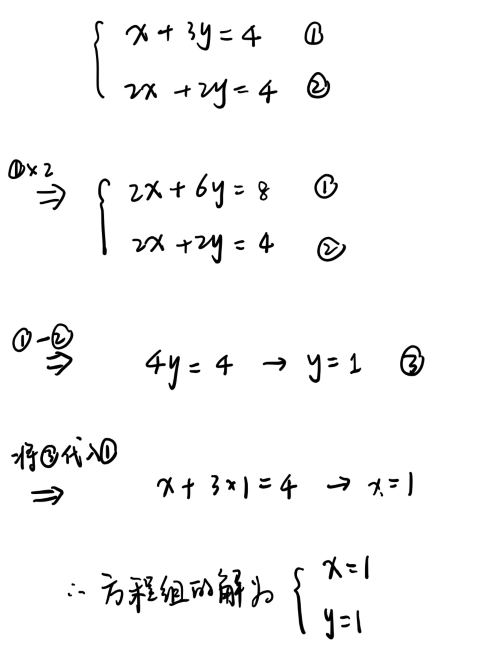
我们可以看到，大致分为消元、代回原式两大阶段。我们将消元、代回原式中用到的操作，总结为以下三个操作：

1.1 同解变形

• 1.用非0的数乘以某方程
• 2.将一个方程的k倍加到另一方程上
• 3.交换两个方程的位置

1.2 增广矩阵

增广矩阵是什么？字面意思看，就是把矩阵给扩大了。确实是这样。

（来自度娘）：增广矩阵（又称扩增矩阵）就是在系数矩阵的右边添上一列，这一列是线性方程组的等号右边的值。

我们一般这么表示它：

$$\overline A {\rm{ = } }\left[ {\begin{matrix} { {a_{11} } }& \cdots &{ {a_{1n} } }\\ \vdots & \cdots & \vdots \\ { {a_{n1} } }& \cdots &{ {a_{nn} } } \end{matrix}\begin{matrix} { {b_1} }\\ \vdots \\ { {b_n} } \end{matrix} } \right]$$

接下来的第二章，可以理解为使用矩阵的语言描述同解变形，并求解方程组。

2. 初等变换、初等矩阵

2.1 由同解变形到矩阵的初等行变换

我们在1.1中介绍了方程组的同解变形，现在把它移植到矩阵上。

• 1.用非0的数乘矩阵的某一行（倍乘）
• 2.将一行的k倍加到另一行上（倍加）
• 3.交换矩阵中两行的位置（互换）

列同理。

2.2 初等矩阵

• 什么是初等矩阵

单位矩阵经过一次初等变换所得到的矩阵称为初等矩阵。

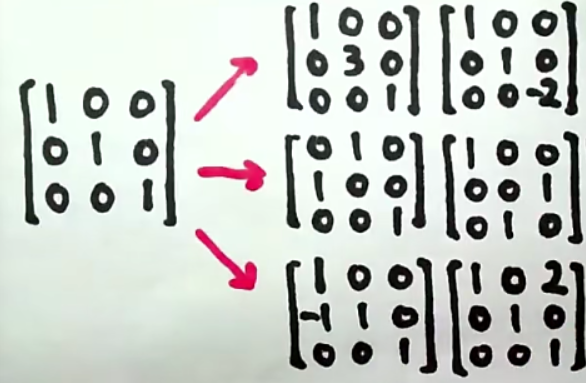
每个初等变换可以有两种理解的方法，即从行变换或从列变换变换而来。

• 初等矩阵的逆

1.倍加矩阵

$${\left[ {\begin{matrix} 1&0&0\\ 0&1&0\\ 0&k&1 \end{matrix} } \right]^{ - 1} } = \left[ {\begin{matrix} 1&0&0\\ 0&1&0\\ 0&{ - k}&1 \end{matrix} } \right]$$

2.互换矩阵

是它本身。

$${\left[ {\begin{matrix} 1&0&0\\ 0&0&1\\ 0&1&0 \end{matrix} } \right]^{ - 1} } = \left[ {\begin{matrix} 1&0&0\\ 0&0&1\\ 0&1&0 \end{matrix} } \right]$$

3.倍乘矩阵

$${\left[ {\begin{matrix} 1&0&0\\ 0&1&0\\ 0&k&1 \end{matrix} } \right]^{ - 1} } = \left[ {\begin{matrix} 1&0&0\\ 0&1&0\\ 0&{\frac{1}{k} }&1 \end{matrix} } \right]$$

2.3 初等变换

初等矩阵$P$左乘矩阵$A$，其乘积$PA$就是矩阵$A$作一次与$P$同样的行变换。

初等矩阵$P$右乘矩阵$A$，其乘积$AP$就是矩阵$A$作一次与$P$同样的列变换。（基本不用）

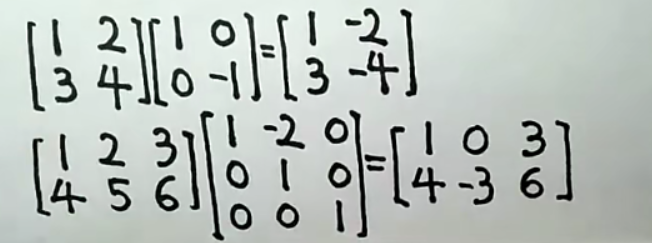
详解：

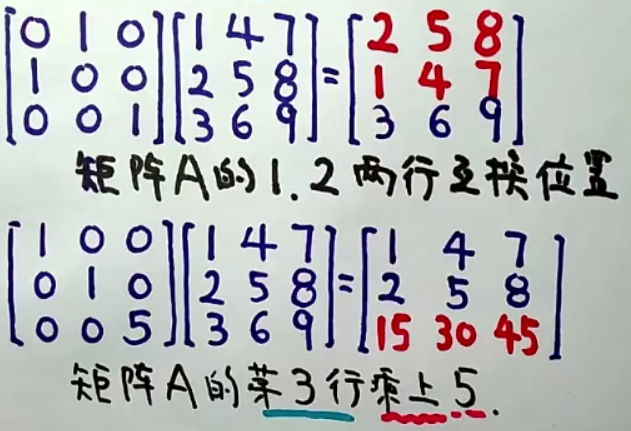
2.4 矩阵等价

• 定义

矩阵$A$经过有限次初等变换变成矩阵$B$，就称矩阵$A$与$B$等价，记作$A \cong B$

• 性质

1. 反身性
   自己等价自己。$A \cong A$
2. 对称性
   若$A \cong B$，则$B \cong A$
3. 传递性
   若$A \cong B$，$B \cong C$，则$A \cong C$

• 等价标准型

定义：经过多次变换以后，得到一种最简单的矩阵，就是这个矩阵的左上角是一个单位矩阵，其余元素都是0，那么这个矩阵就是原来矩阵的等价标准型。（摘自度娘）

只要不是0矩阵，一定能够化成这种形式

2.5 行阶梯矩阵

• 定义

设$A$是m*n的矩阵，若满足
（1）矩阵如果有零行，则零行都在矩阵的底部。
（2）每个非零行的主元（即该行最左边的第一个非零元）所在列的其他元素都为0。

用人话讲，就是矩阵中每一行的第一个不为零的元素的左边及其所在列以下全为零。

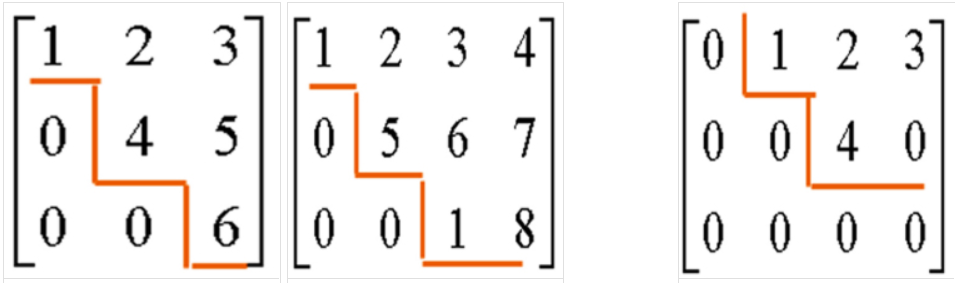
• 行最简矩阵

设$A$是m*n的矩阵，若满足$A$是行阶梯矩阵，且非零行的主元都是1，且主元所在列其他元素都是0，则$A$是行最简矩阵。

行最简矩阵有什么用？先埋个伏笔。

2.6 用初等行变换求逆矩阵

• 可逆的充要条件（喜+1）

A可逆等价于A可表示为若干初等矩阵的乘积。

• 定义一个新矩阵

$$(A|E) = \left[ {\begin{matrix} A&E \end{matrix} } \right]$$

• 怎么求出逆？

通过初等行变换，将A矩阵化为单位矩阵，则E矩阵部分就是A的逆了。

注意：初等行变换是对整个矩阵做的。而结果是分开看的。

• 原理？

当A进行初等行变换→PA=E，则P=A的逆

与此同时E进行相同的初等行变换→PE=P=A的逆

2.7 求解方程组

2.7.1 直接法

有$AX=B$，若$A$可逆，则$X=A^{-1}B$

但还要进行矩阵乘法，计算量比较大，所以又引入初等行变换法。

2.7.2 初等行变换法

有$AX=B$，若$A$可逆，则$X=A^{-1}B$
由$PA=E,PB=A^{-1}B=X$，我们使用增广矩阵的形式表示它：

$$P(A,B)=(E,X)$$

我们看一道例题：

首先，依照结构构造$P(A,B)$，对整个矩阵初等行变换，将$A$变为单位矩阵，$B$部分就是方程的解了。

2.7.3 高斯消元解方程组

• 步骤

1.从上往下正向消元，化为阶梯型矩阵。

正向消元，就是使用$a_{11}$对$a_{21}$~$a_{n1}$进行消元，第二列使用$a_{22}$对$a_{32}$~$a_{n2}$进行消元，总结起来就是使用主对角线上的元素对它下面的元素进行消元，变成阶梯型矩阵。（期间可能会使用同解变形）

2.从下往上反向求解，带回原式。

变成阶梯型矩阵后，我们就可以进行反向求解了。

3.例题

• 自由变量

方程组有无穷多解时，需要对自由变量进行赋值。自由变量使得这个方程组有确定的解。

确定方法：把系数矩阵化成行阶梯型，非零行的首个非零元对应的列就是主元，其余的都是自由变量。

至此，我们已经可以解方程组了。但，我们对比克拉姆法则，其不仅可以解方程组，还可以判断解的个数，所以接下来的工作就是判断解的个数。

3. 矩阵的秩（敲坏黑板）

3.1 概念

• 子式的概念

在$m*n$的矩阵$A$中，任取k行与k列($k \le m,k \le n$)，位于这些行与列的交叉点上的$k^2$个元素按其在原来矩阵$A$的次序可以构成一个$k$阶行列式，称其为矩阵$A$的一个$k$阶子式。

其实就是抽$k$行抽$k$列，取交集，得到$k^2$个数，这些数按原来的次序组成行列式，就叫做$k$阶子式。

例子：

• 秩的概念

若矩阵$A$中存在r阶子式不为0，$r+1$阶（如果存在）子式全为0，则称矩阵$A$的秩为$r$，记成$r(A)=r$。

零矩阵的秩规定为0。

使用自然语言描述：

3.2 公式

1. $$0 \le r({A_{m*n} }) \le \min (m,n)$$
2. $$r({A^T}) = r(A)$$
3. $$r(A + B) \le r(A) + r(B)$$
4. $$r(kA) = r(A)$$
5. $$r(AB) \le \min (r(A),r(B))$$
6. 若$P,Q$可逆，则$r(PAQ)=r(A)$,$r(PA)=r(A)$,$r(AQ)=r(A)$
7. $$r\left[ {\begin{matrix} A&0\\ 0&B \end{matrix} } \right] = r(A) + r(B)$$
8. $$\max (r(A),r(B)) \le r(A|B) \le r(A) + r(B)$$

3.3 定理

经过初等变换矩阵的秩不变。

即3.2中的第6个公式。

同型矩阵秩相等则等价。

有了秩这个工具，就可以打最后的boss了。

4. 线性方程组有解判定

4.1 定理

矩阵方程$AX=B$有解等价于$r(A)=r(A|B)$。

4.2 非齐次方程组

1.无解

$$r(A) + 1 = r(\overline A )$$

2.唯一解

$$r(A) = r(\overline A ) = n$$

-$n$是方程未知数的个数啦，也就是元数。

3.无穷解

$$r(A) = r(\overline A ) < n$$

4.3 齐次方程组

1.零解

齐次方程组一定有解。且不是零解就是无穷解。

$$r(A) = r(\overline A ) = n$$

2.无穷解

$$r(A) = r(\overline A ) < n$$

总结

第二章与第三章其实都是在讲矩阵这个新算子，并且讲这个新算子应用到线性方程组的计算中。为了算子的计算封闭性等性质，提出了逆矩阵、转置矩阵等等，其目的都是为了使矩阵的运算是可以进行的。第三章将第二章所述的性质综合应用，并使用矩阵来解决线性方程组的解。

第二章中，首先提出了矩阵的概念与矩阵的类型，既然有了算子，自然就要定义计算法则。接下来就是讲矩阵的运算法则，有矩阵加法、乘法（分为数乘与矩阵乘法）、转置。最后还有矩阵的逆，我们可以理解为实数域中的倒数。为了求逆，我们还提出了伴随矩阵。将运算法则阐述完后，我们将分治或是降维的思想应用到矩阵，提出了分块矩阵。

第三章中，由高斯消元法引出初等变换，我们使用初等变换可以求出矩阵的逆，从而求出方程组的解。我们可以使用初等变换与增广矩阵的思想，直接求解出方程组的解。我们可以使用高斯消元法的基本思想，直接对矩阵进行初等变换，同样可以求解出方程的解。与克拉默法则一样，矩阵解法同样也能够判断解的个数，于是提出了秩的概念，通过秩，可以判断方程组是否有解，解的个数。