到第四章啦,这章比第三章还要难,枯了。
下面我会尽量把向量这一章的内容解释清楚。
1. 概念
1.1 定义
- n个数构成的有序数组称为n维向量。
1.2 表示

列向量可以有转置的写法,比较省空间。
1.3 零向量
如果向量的所有分量都是0,就称它是零向量。
记作
1.4 向量相等
前面第三章矩阵,我们说了矩阵相等的概念。向量可以理解为特殊的矩阵。
所以,向量相等的概念与矩阵相等的概念是一样的。
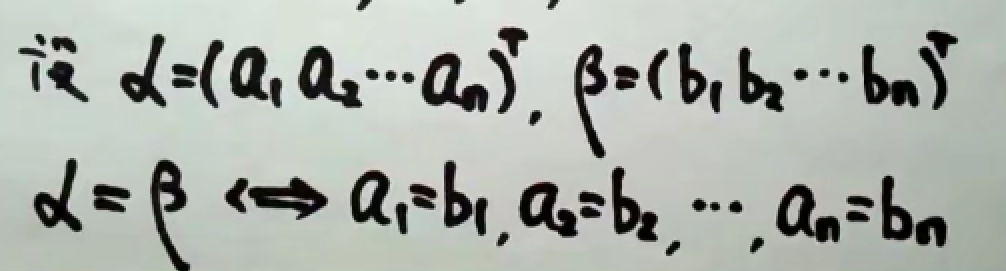
1.5 运算
P.S. 把向量理解为只有一行或一列的矩阵,则矩阵有的规律,向量也有。
I.向量加法

即对应位置相加,与矩阵相加是一样的。
它的几何意义就是我们熟知的力的合成(对角线法则)。
II.向量数乘

与矩阵数乘也还是一样的(doge),对每一维乘以一个常数。
特别地,常数为0时,
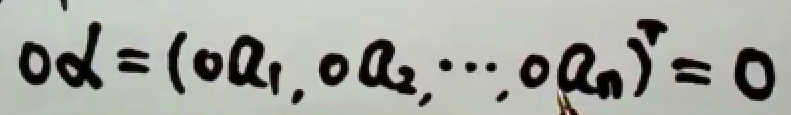
2. 线性表示
2.1 向量线性表示的定义
I.

II.

根据I、II,我们可以得出向量线性表示的定义。
III.例题
已经有了向量线性表示的定义,现在就来实战一下:

用观察法求得系数。
IV. 三种情况
一共有两大种情况,可以线性表示与不能线性表示。可以线性表示又分两种情况,有唯一表示和无穷表示。所以一共是三种情况。
- 不能线性表示

- 唯一线性表示

- 无穷线性表示
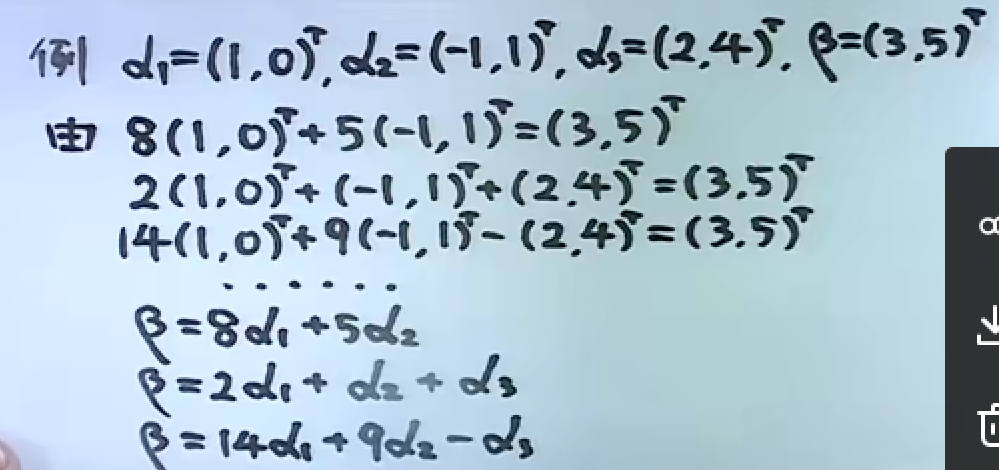
2.2 向量线性表示的方法论
我们可以看到,上面用了观察法求得向量的系数。显然是行不通的,数据不可能都这么简单。2.2中,我们要做的就是找出求解表示系数的方法。
2.2.1 定理

这是把我们2.1的定义浓缩了一下,变为简洁的数学表达。
2.2.2 引例
接下来通过一个栗子,把我们之前学习求方程组的解与求线性表示系数联系到一起。

首先,我们依据定义,写出对应的表达式:
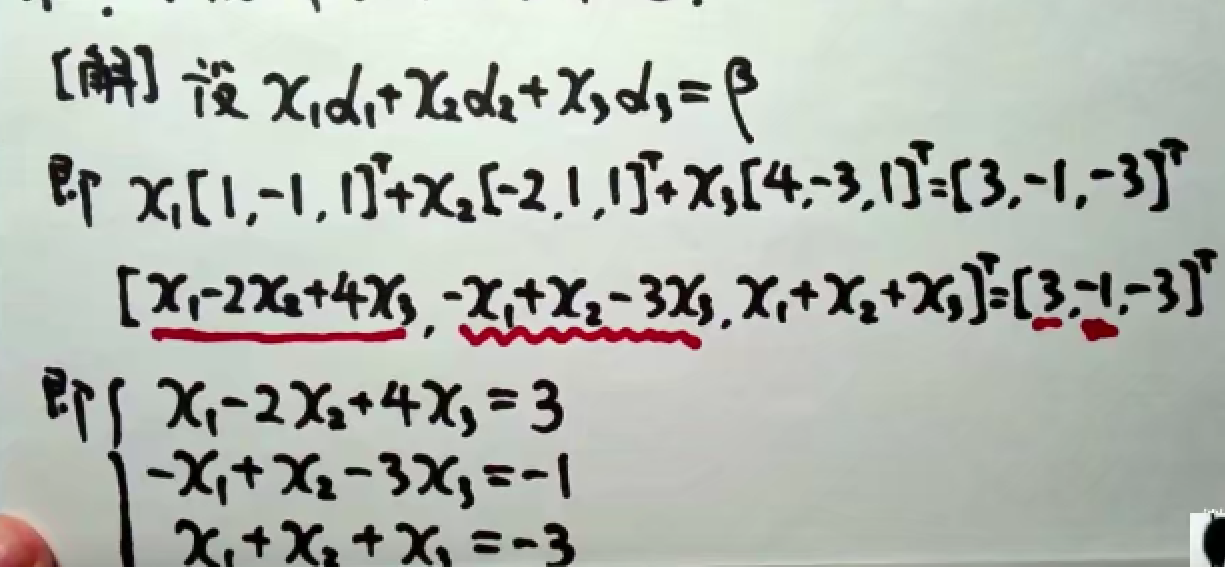
将表达式展开,依据向量相等的定义,我们得到非齐次方程组。
先说结论:
如果方程组无解,说明得不到一组k值使得能够被线性表示。
如果方程组有唯一解,说明只有一组k值使得能够被线性表示。
如果方程组有无穷解,说明有无穷组k值使得能够被线性表示。
与2.1的三种情况是对应的。
将方程组写成矩阵的形式,化简,求解。

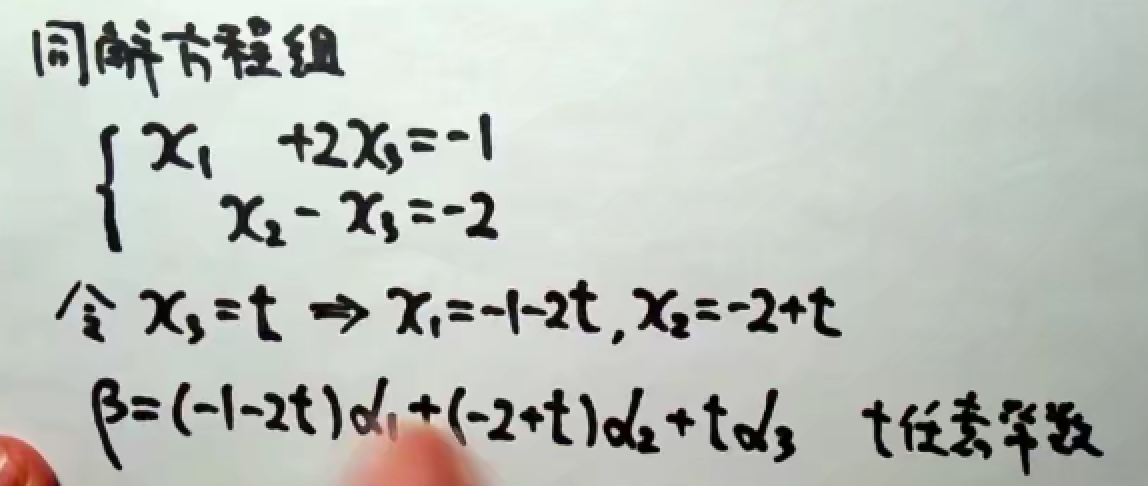
最后该题的答案是无穷解,并得出了表达式。
2.3 向量线性表示的题型
题型1:确定能否线性表示
由引例,我们可以知道,能够进行线性表示的前提是方程组有解。
方程组有解我们有两条路可以走:
1.克拉默法则
适用于未知数个数与方程数相等的情况(行列式)。可以通过直接求解系数行列式,如果D的值不等于0,说明有唯一解。否则,根据矩阵的秩确定是无解或是无穷解。
2.矩阵(推荐)
写出增广矩阵,化简到最后。如果有解(系数行列式的秩等于增广矩阵的秩),说明可以进行线性表示。否则,是不能进行线性表示的。
题型2 :已知可以线性表示,求系数
我们使用矩阵法,去解方程组。
写出增广矩阵,化简到最后。如果秩小于未知数个数,有无穷解,说明有无穷个线性表示的方法;否则,只有唯一一种表示方法。
例子:



2.4 向量组线性表示
2.4.1 定义
我们上面说了向量线性表示的定义,现在将向量拓展到向量组。

其实很简单,把向量组中的每个向量应用一遍向量线性表示的定义,如果都符合,那就满足向量组的线性表示。原来是1toN的关系,现在是NtoN的关系。
如果互相都能线性表示,则说明它们等价。
来看两道例题:

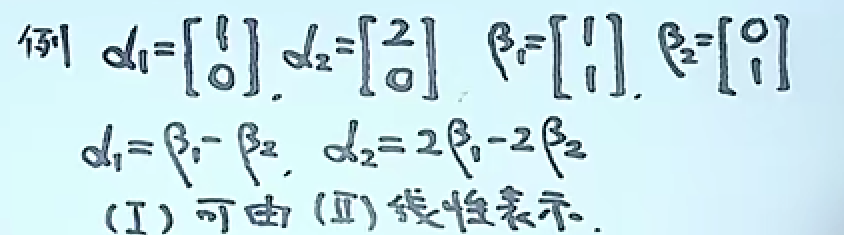
注意:向量的等价与其组成的矩阵的等价没有必然联系!

性质:向量组线性表示具有传递性。

2.4.2 定理

简单证明如下:
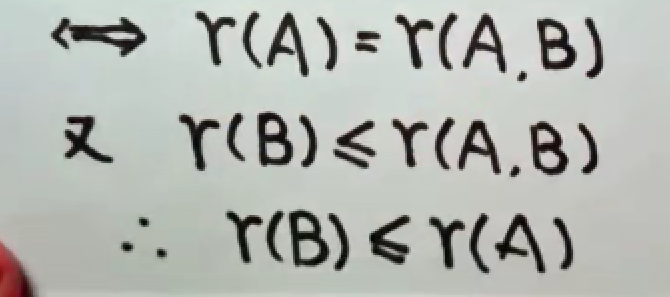
推论:
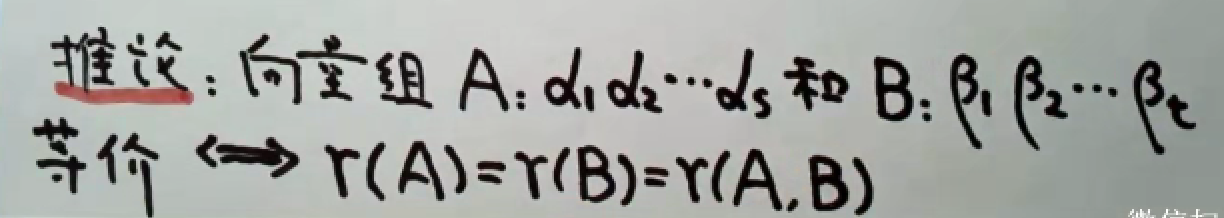
来个栗子~
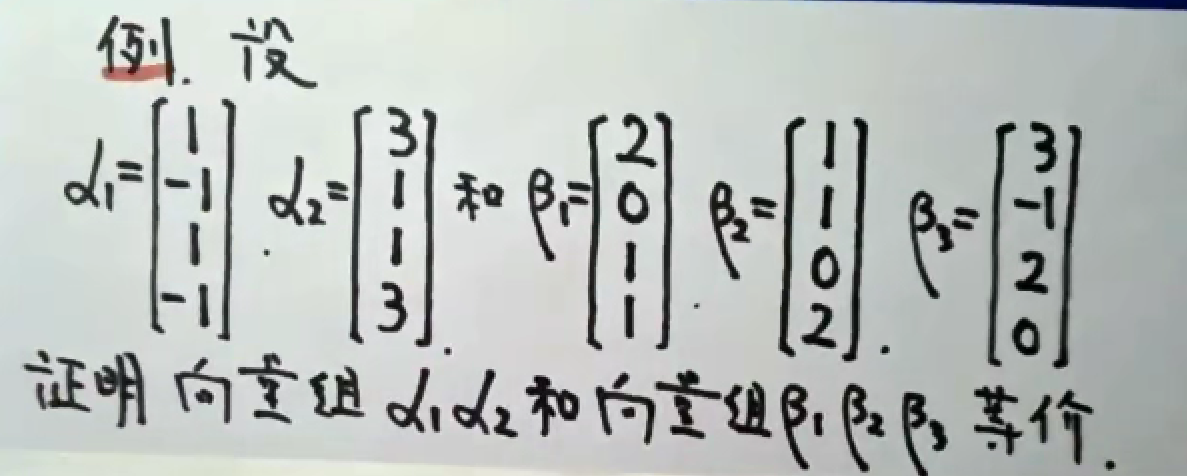
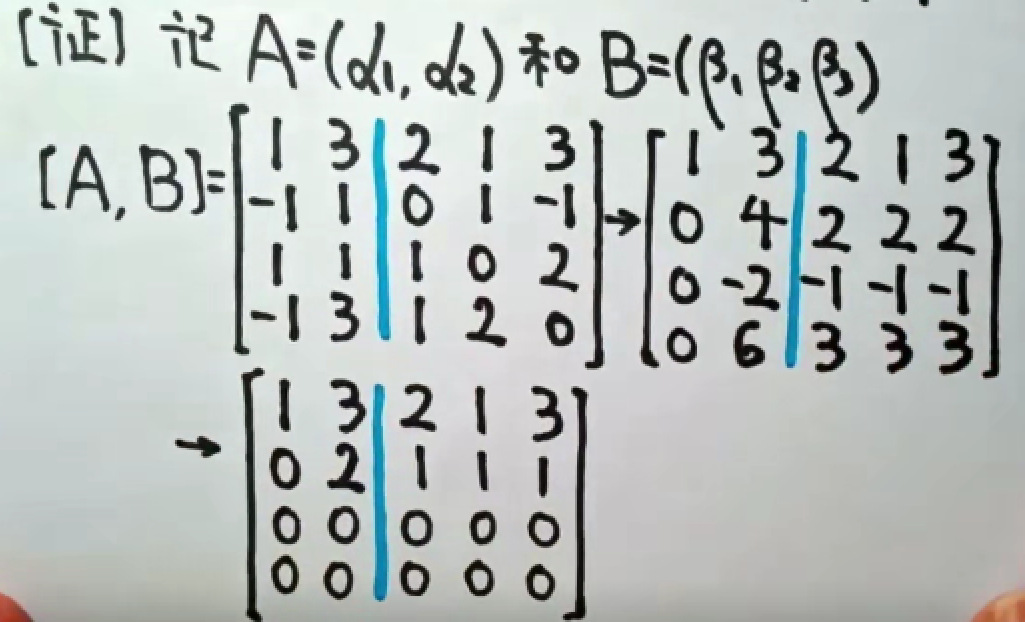
3. 线性相关、无关
3.1 定义

如果都为0,说明这些向量线性无关,否则说明这些向量线性相关。
特别地,
1.如果一个向量组中含有零向量,则向量组必线性相关。
2.如果一个向量组中有两个向量各分量都成比例(向量共线),则向量组必线性相关。
几何意义
线性相关
- 二维向量共线、三维向量共面
- 零向量与其他向量都共线
- 零向量与其他向量一定相关
线性无关
- 向量相互垂直
例题
下面看几题例题,直观感受一下求解过程。



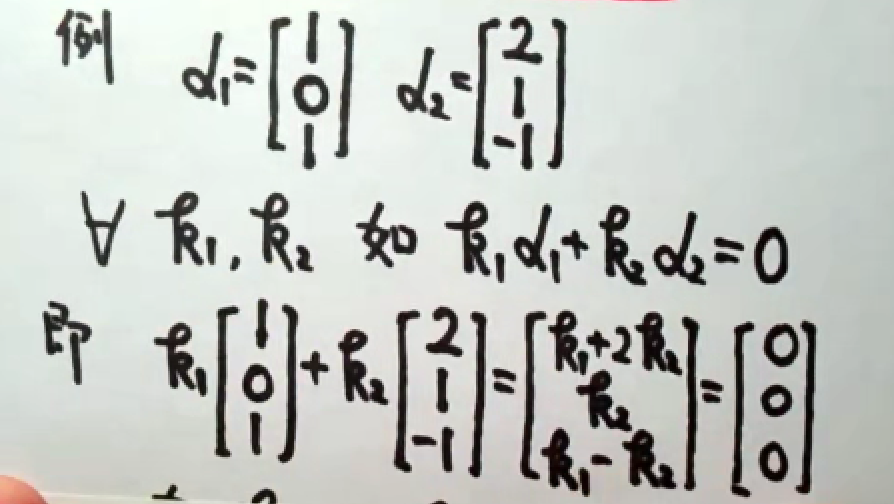

可以看到,我们只能用观察法求解,效率低下。现在,我们也要将求解系数总结为方法论。
3.2 方法论
引例
与之前一样,我们通过引例来总结方法论。

根据定义,我们写出对应形式,再根据向量相等的定义,展开为齐次方程组:

将齐次方程组中的系数矩阵写出来:

因为矩阵的秩小于未知数的个数,所以有非零解;即线性相关。
方法论
首先,根据定义写出齐次方程组。
接着,我们就要判断是有无非零解。
当方程个数与未知数个数相等的时候,用克拉默法则。如果D=0,说明有非零解, 线性相关;否则线性相关。
也可以使用矩阵求解齐次方程组,如果秩小于未知数个数,说明有非零解,线性相关;否则线性无关。
P.S.判断向量线性相关时,一定要转换为列向量。即使题目给的是判断行向量的线性相关。
3.3 定理
3.3.1 定理1

警惕:

并不一定能被线性表示。三个向量中至少有一个可以被表示,并不知道是哪个。这个因果关系是不对的。
3.3.2 定理2

反证法可以证明这个定理。
3.3.3 定理3

推论:

用途:判断向量个数
3.3.4 推论1
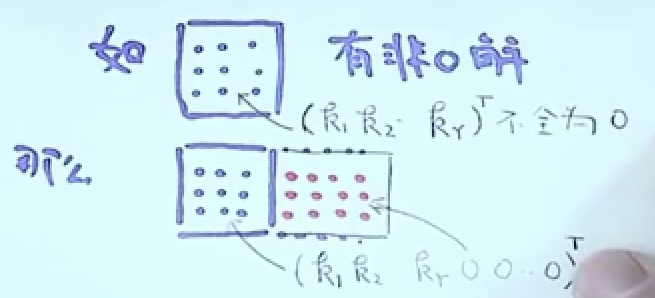
如果原方程组有非零解,现在添加未知数,那么现在这个方程组还是有非零解。
因为添加后,解依然还是要满足原来的方程组。
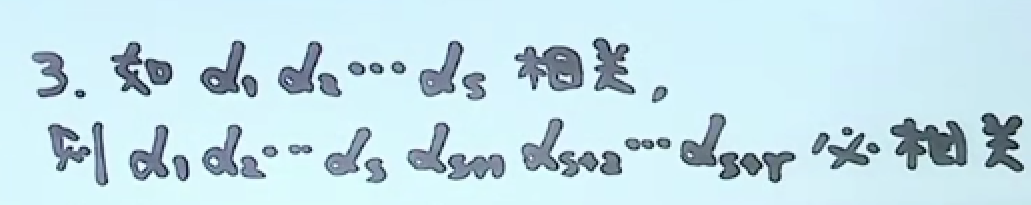
子集合相关 整体相关。
3.3.5 推论2
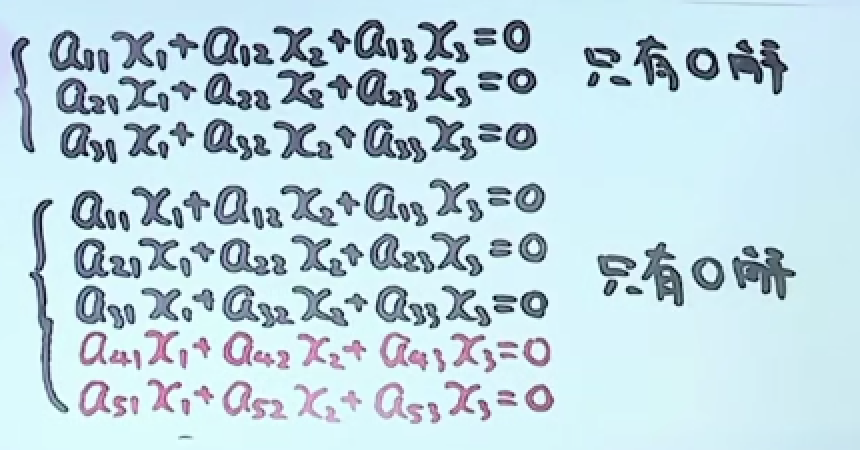
如果原方程组只有零解,现在添加方程个数,那么新方程组依然只有零解。
因为添加后,解依然还是要满足原来的方程组。
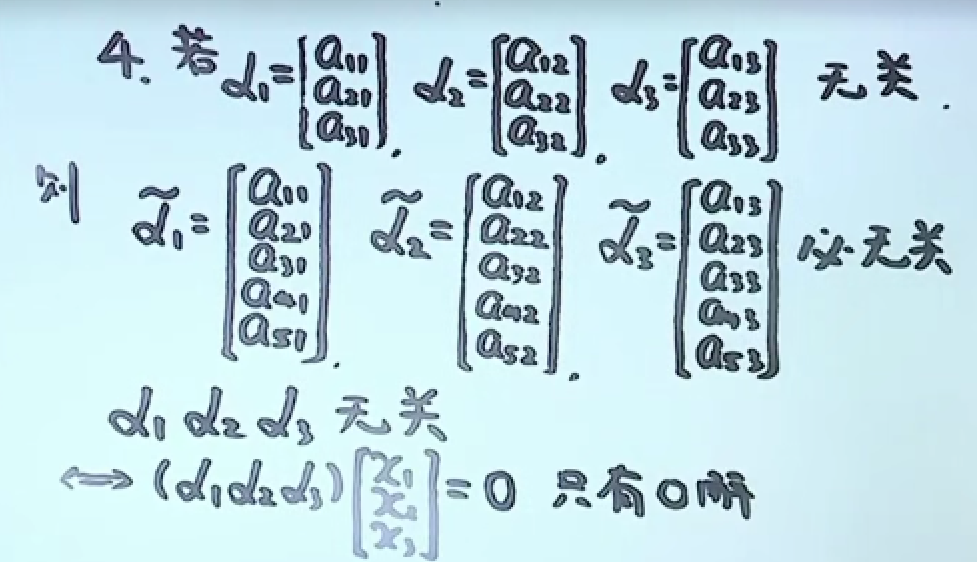
低维无关,高维必无关。
3.4 线性无关的证明题
使用定义:
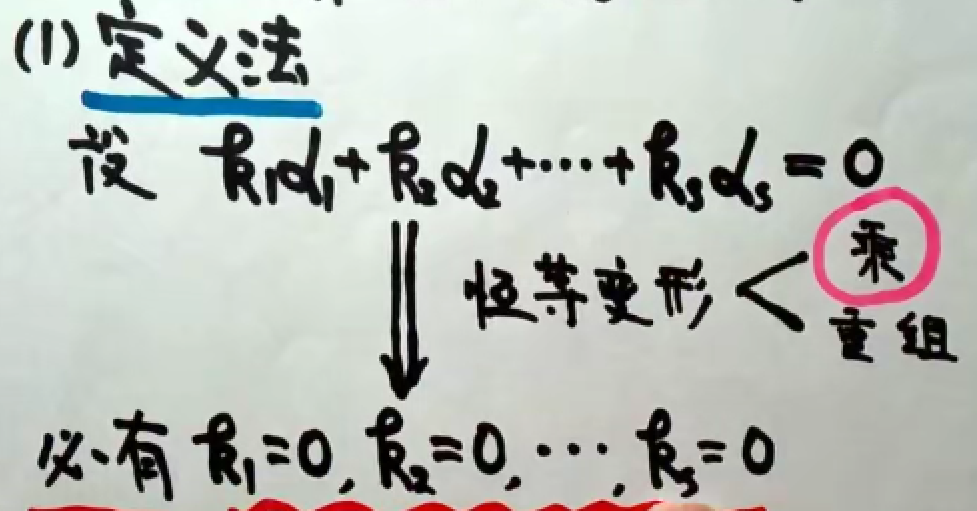
例1:


4. 向量组的秩
我们前面也提到了矩阵的秩,事实证明,向量组的秩和矩阵的秩是有一定关系的。我们研究向量组的秩,是为了更好表述无穷解时的情况。
为了引入向量组的秩,我们先引入极大线性无关组的概念。
4.1 极大线性无关组
定义
极大线性无关组很重要,不仅关系到秩,还关系到后面的向量空间。

等价定义:

简单来说,就是从一个向量组中取出s个向量,这s个向量是线性无关的。且再从向量组中取一个向量组成s+1个向量,这s+1个向量是线性相关的。这时候我们就称前面的s个向量是极大线性无关组,极大体现在,无关体现在这s个向量是线性无关的。
注意点
1.极大线性无关组的s个成员不唯一,但一定有s个成员。
来源于定理:

2.

3.如果向量组本身线性无关,则这个向量组本身就是自己的极大线性无关组。

求解方法
见4.2
4.2 向量组的秩
定义

说白了,4.1求的极大线性无关组中的s(也就是成员数)就是向量组的秩。
例子

向量组的秩为2。
4.3 补充定理
定理1
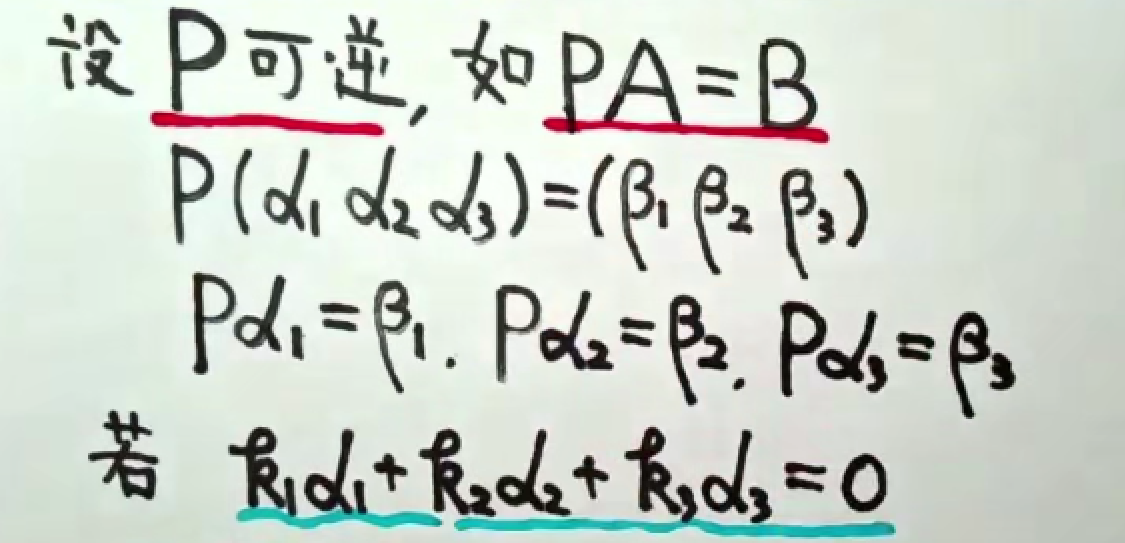


这个定理用人话说就是,一个矩阵通过初等变换到另一矩阵,保持了相同的线性相关性,可以用相同的线性表示。而初等行变换在这里使用P矩阵代替了,只要P矩阵可逆,这个定理就成立。
定理2:三秩相等

这个定理将矩阵的秩与向量组的秩关联在一起,矩阵的秩等于行向量组的秩,也等于列向量组的秩。
定理3

子集的秩一定小于等于整体的秩。
定理4

与2.4.2相同。
4.4 求秩与极大线性无关组
引例
一般来说,求秩与求极大线性无关组是捆绑在一起考的。

根据定理2,我们把列向量组成矩阵,秩不变。
根据定理1,我们将矩阵进行初等行变换,并变为最简形(可选)。

这时,我们看着右边的矩阵,很轻易的就可以观察出秩与极大线性无关组。观察得出线性无关(不唯一),由定理1,线性无关。矩阵的秩为3,则矩阵的秩也为3。

最后,用极大线性无关组去表示剩余向量。这个也是用矩阵来做,但是答案要写成矩阵的形式。同样由定理1可知。

方法论
首先,把向量恢复成矩阵A。(定理2)
接着,将矩阵A进行初等行变换,变为简单的矩阵B。(定理1)
用矩阵B求解出秩、极大线性无关组、表示其余向量。下标不变,将B换为A。(定理1)
结束。
5. 基础解系
在引入向量的秩的时候,我们说引入向量的秩是为了更好表述无穷解时的情况。
第5章与第6章就是对秩的应用了,而第5章针对的是齐次方程组,目的:用有限解描述齐次方程组的无穷解。即一个不落的表示无穷解(非零解)。
5.1 齐次方程组解的性质
性质1
常数倍的原解仍是方程组的解。
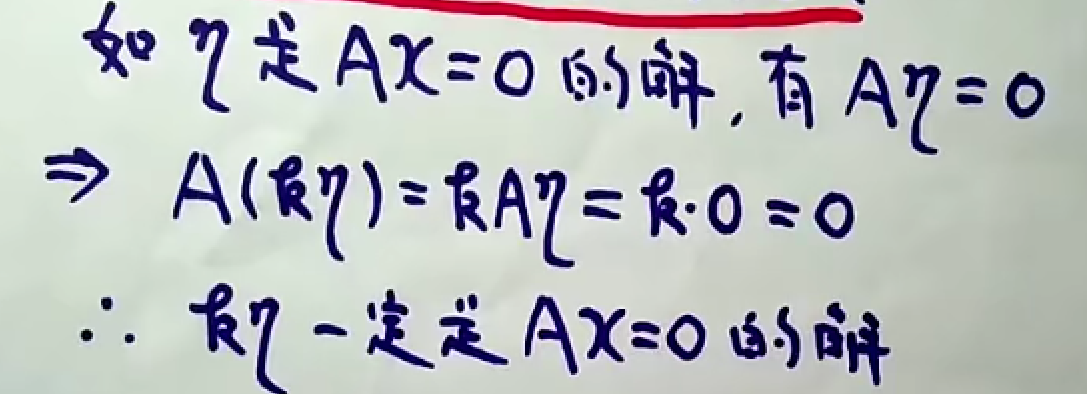
性质2
常数倍解的线性组合仍是方程组的解。
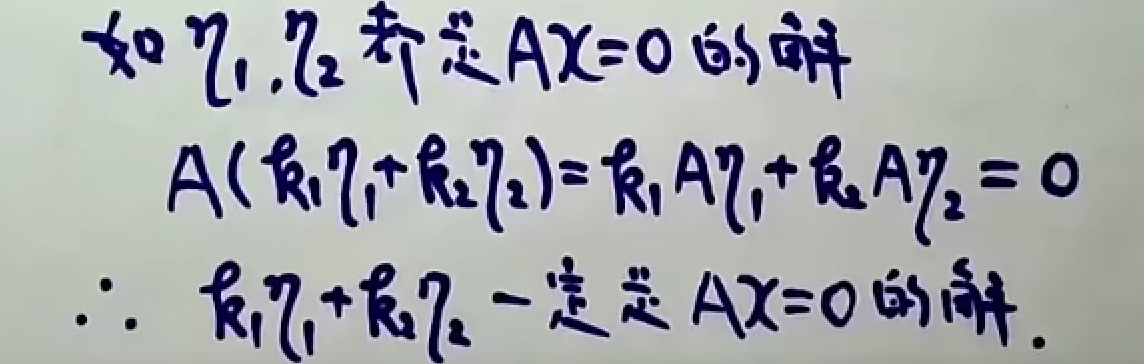
5.2 补充定理

其实就是运用第四章的内容啦。求解出极大线性无关组,将其余向量用极大线性无关组表示。
5.3 基础解系
定义
由5.2的补充定理,我们很自然的引出了基础解系的定义。其实讲的都是废话= =就是找解集中的极大线性无关组,并用其表示剩余向量,组成的解称为基础解系。

例题1

首先,进行初等行变换。

确定基础解系的向量个数。

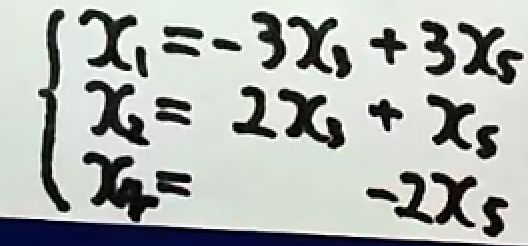
赋值。

得到基础解系。(红字的地方说明这两个向量是是线性无关的)

得到通解。
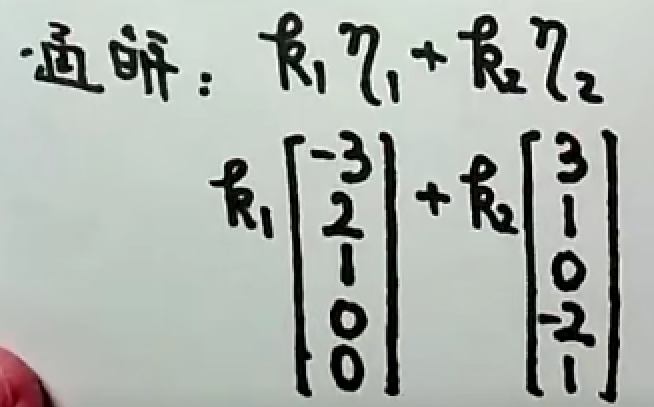
例2
化为阶梯型矩阵,并确定基础解系的向量个数。

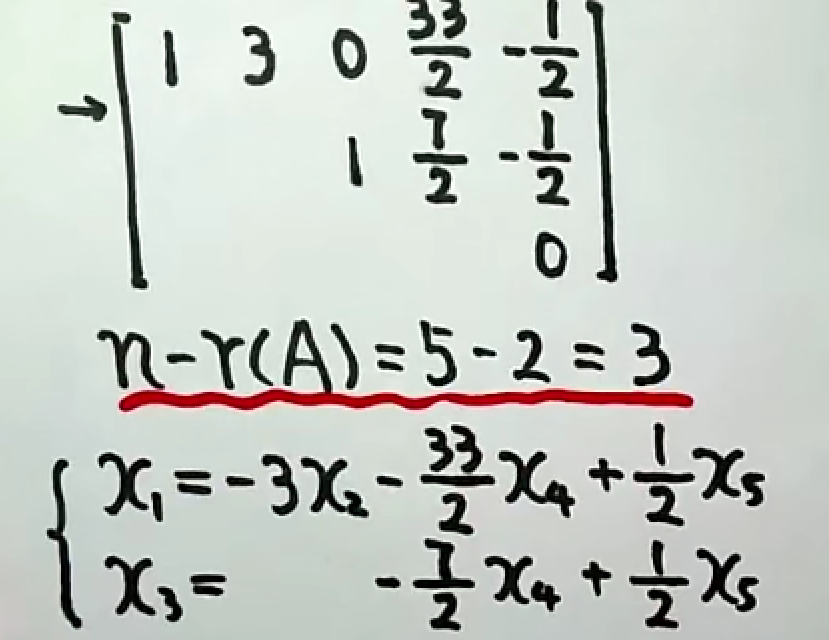
赋值。

带回。

方法论
先做初等行变换,变为阶梯型。
接着写出同解方程组,确定极大无关组的个数及成员。
赋值,带回,得到基础解系。
6. 解的结构
第五章是对齐次方程组无穷解的描述,第六章则是对齐次方程组无穷解的描述。
6.1 导出组
定义
首先引入导出组的概念。


简单来说,导出组就是把非齐次方程组的常数项硬改成0了….这样就是齐次方程组。这就是导出组。
性质
1.

2.

6.2 解的结构
定义

简单来说,就是非齐次线性方程组解的结构包括特解与基础解系。特解并不是唯一的,基础解系也不是唯一的。而解怎么求呢?
引例1

首先,将矩阵化为阶梯型,求出基础解系的个数。

写出同解方程,赋值求出特解。
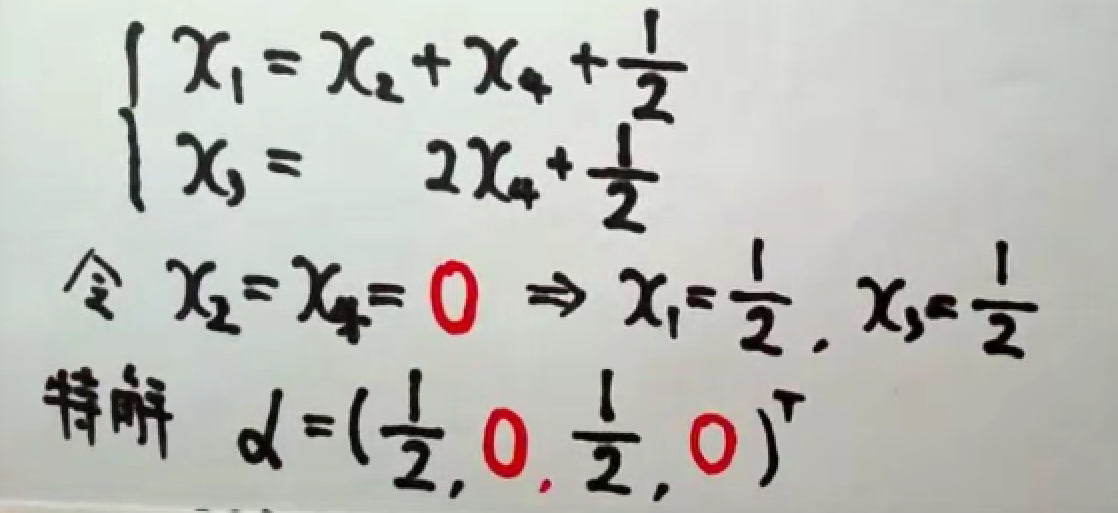
赋值求出基础解系。
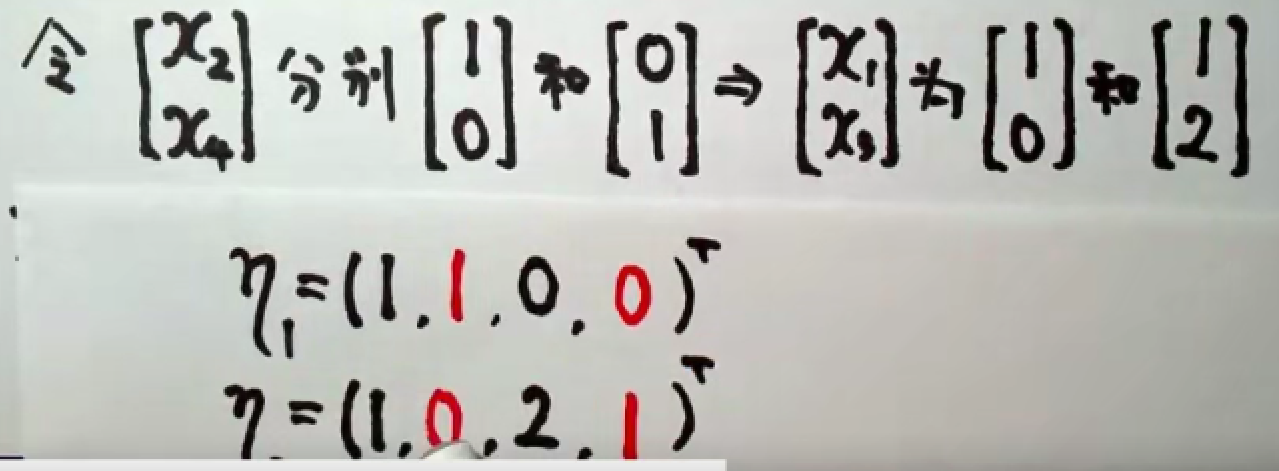
将特解加上基础解系就是通解了。
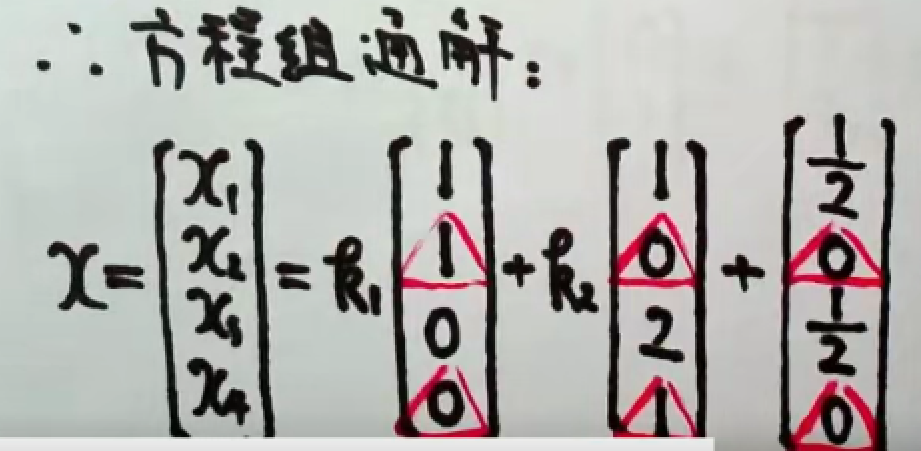
引例2:带参数求通解


1.无解

2.无穷多解


3.唯一解
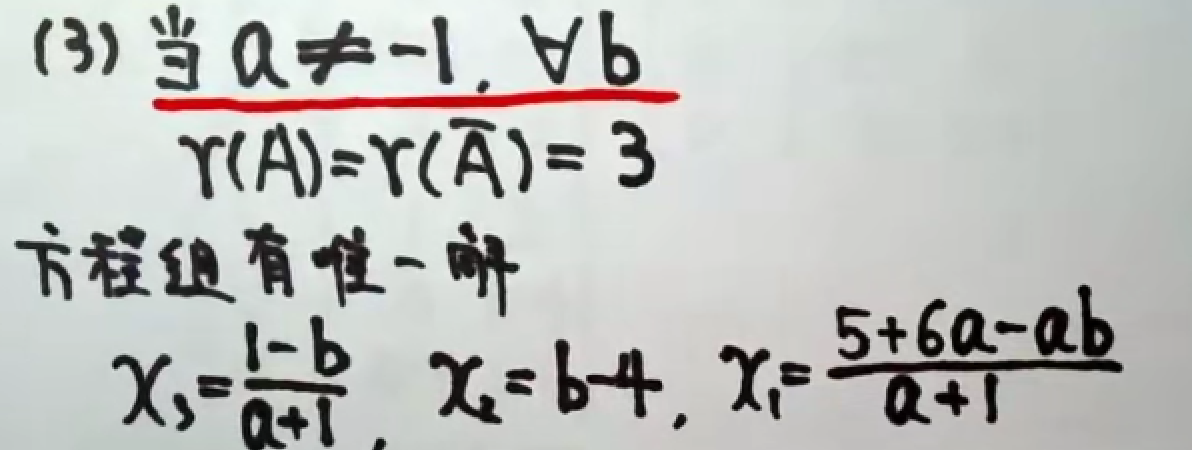
方法论
其实求非齐次方程组解只比齐次方程组多了一步,就是求特解。其余见第五章。
7. 向量空间
7.1 向量空间的定义

这个概念很抽象…..拿离散数学举个例子,有一种运算叫mod,它不管怎么运算(使用集合内的元素),答案也肯定在集合里。这里的向量空间也是这个意思,向量集合中使用加法、数乘,最后结果还在这个集合中,形成闭包。
例子

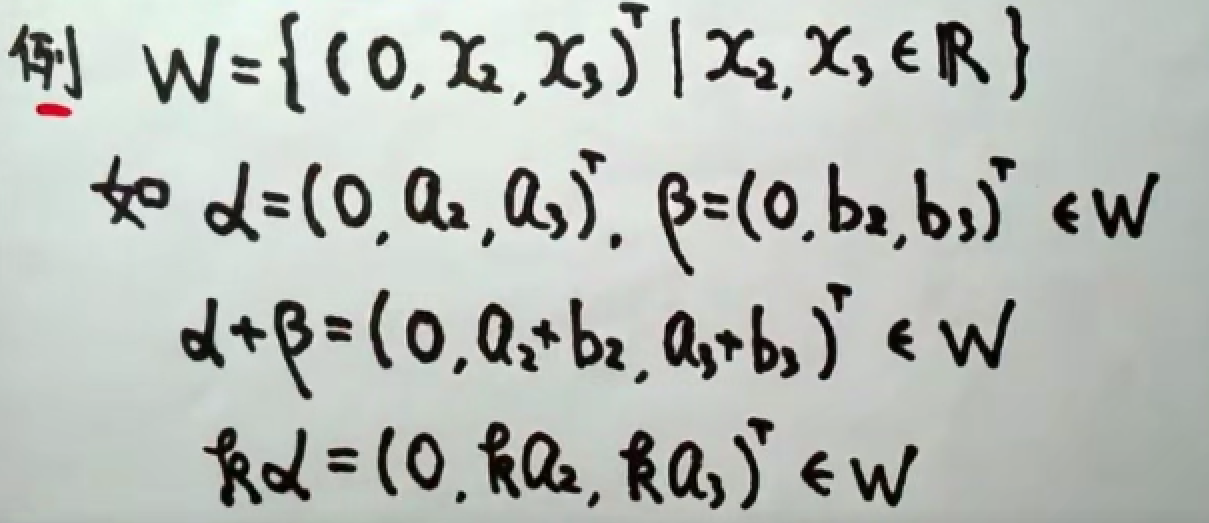



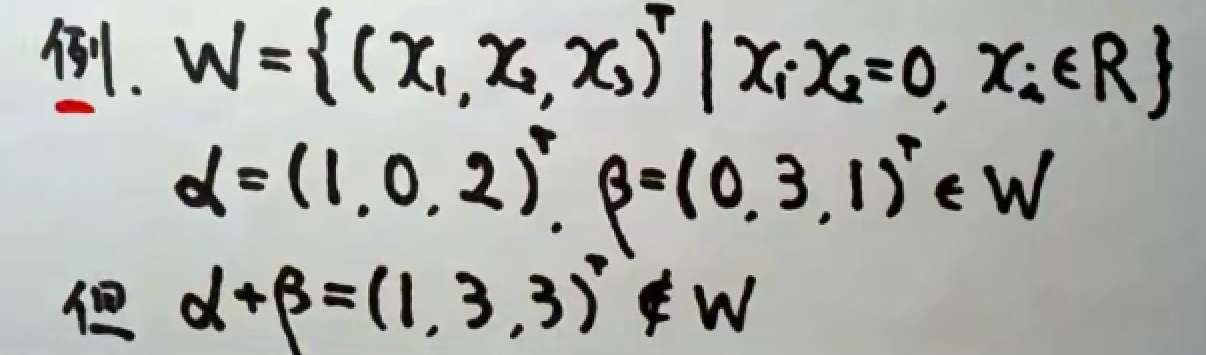
7.2 基
定义

有没有一丝熟悉,基不就是极大无关组吗(doge),换了层皮罢了。不过区别还是有的,之前说的极大无关组对于的向量集合而言,是有限个向量;而这里的向量空间V是无限个向量,所取的父集合不太一样。

又来了,维数相当于向量组的秩。
例题

欲验证是基,就需要验证它在向量空间内,且是线性无关的。

化简,得出坐标。

注意,这里向量是三维向量,但是是二维空间。因为只有两个向量。空间维数与向量维数没有关系。
规范正交基

7.3 坐标变换
7.3.1 过渡矩阵
定义


例题

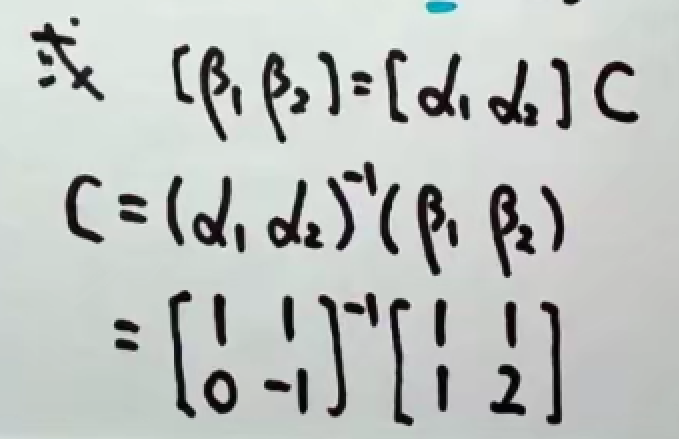
7.3.2 坐标变换公式
定义

例题




