最后一章啦!这一章的内容和前面既独立也不独立,难度还可以。
1. 二次型
1.1 二次型的定义
二次型(quadratic form):n个变量的二次多项式称为二次型,即在一个多项式中,未知数的个数为任意多个,但每一项的次数都为2的多项式。(来自度娘)
举个例子…
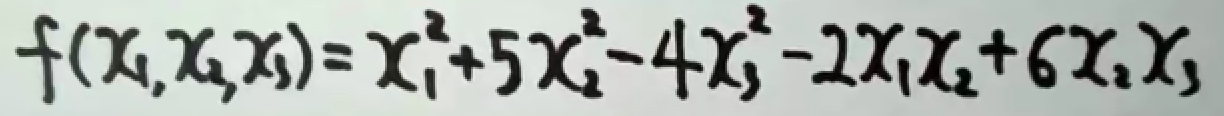
就是未知数的次幂始终是2,这就是二次型。
通过矩阵来研究二次函数(方程),这就是线性代数中二次型的重点。
较为官方的定义:
因为二次函数(方程)的二次部分最重要,为了方便研究,我们把含有 个变量的二次齐次函数:
称为二次型。
1.2 二次型的矩阵表示
我们可以通过矩阵来表示二次型:
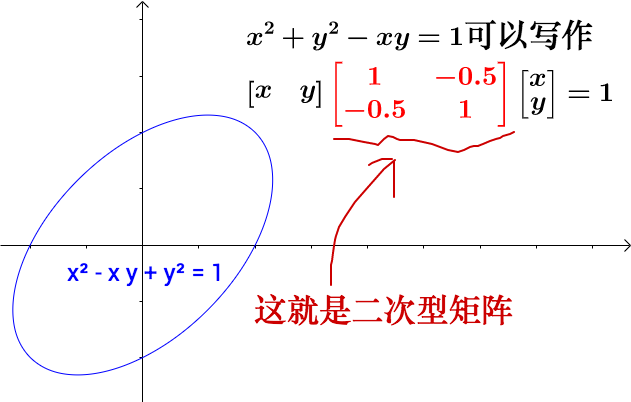
更一般的:

可以写成更线代的形式:
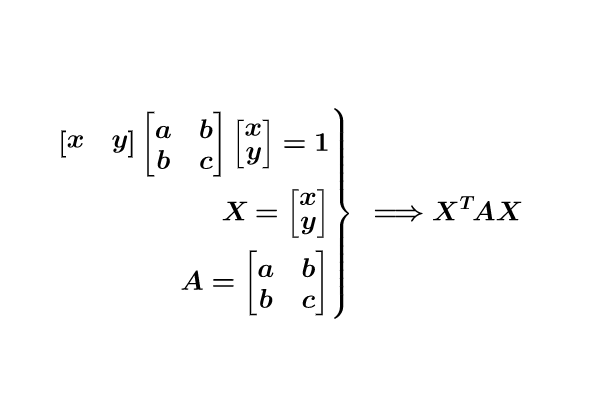
所以有下面一一对应的关系:
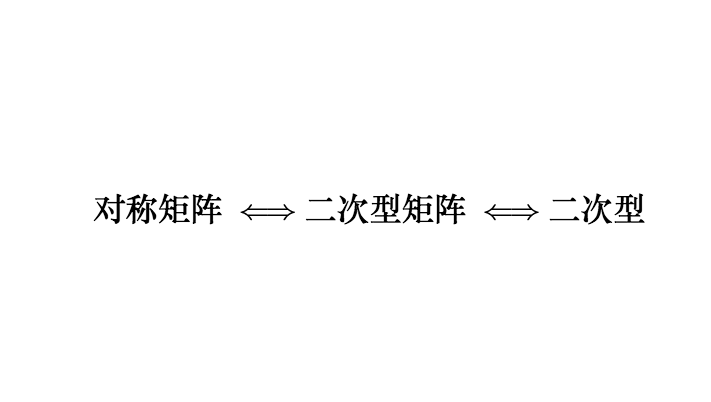
在线代里面,就是通过一个对称矩阵,去研究某个二次型。
1.3 二次型的秩

对称矩阵A的秩就是二次型的秩。
2. 标准型
2.1 定义
一个只含有平方项的二次型称为标准形。就是二次型中的一种特殊情况。

例如上面这个式子…我们就可以称它是标准型。至于为什么出现了对角矩阵…待会揭秘!
2.2 标准型的几何含义
标准的二次方程在直角坐标系下的图像
如果坐标系是一个直角坐标系,相信大家都知道标准方程的图像:


2.3 为什么需要标准型
- 首先,一个标准的二次方程的图像是容易知道的;
- 其次,利用非退化的线性替换可以将一个未知图像的放到一个坐标系(线性替换矩阵)中,使得图像的方程变成标准形;
- 最后,利用这个方程的标准形的图像便可以得到了原方程的图像。
3. 规范型
3.1 定义
在标准型的基础上,系数只有+1或-1的标准型称作规范形。

3.2 二次型、标准型、规范型的转换
3.2.1 二次型to标准型
法1.配方法
例1.

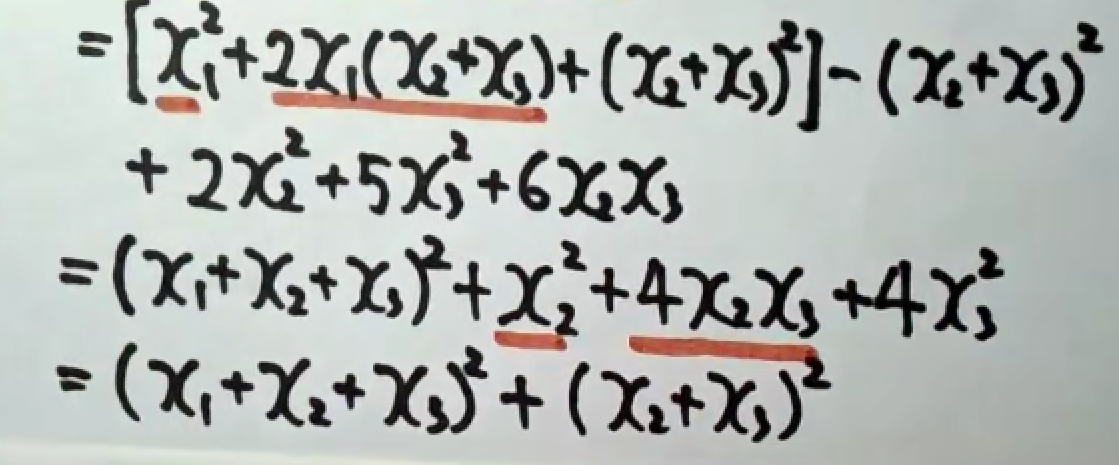
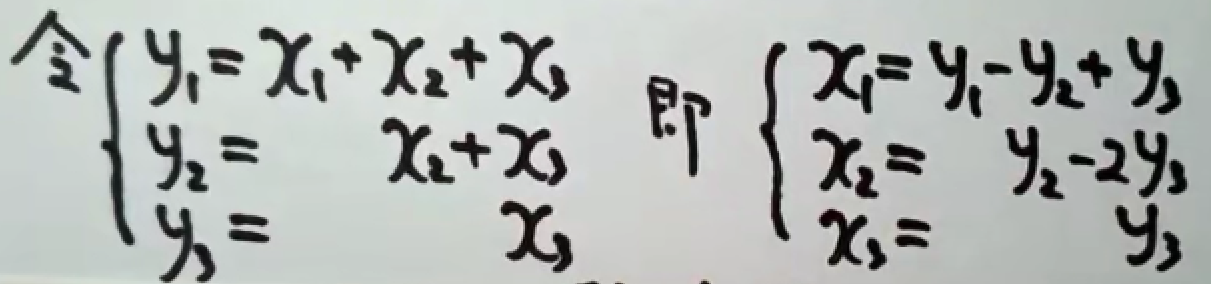
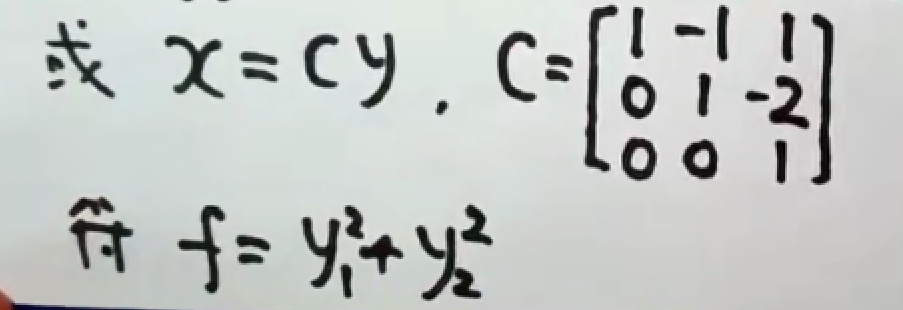
例2.

tips: 没有平方项的二次型,需要自己制造平方项。
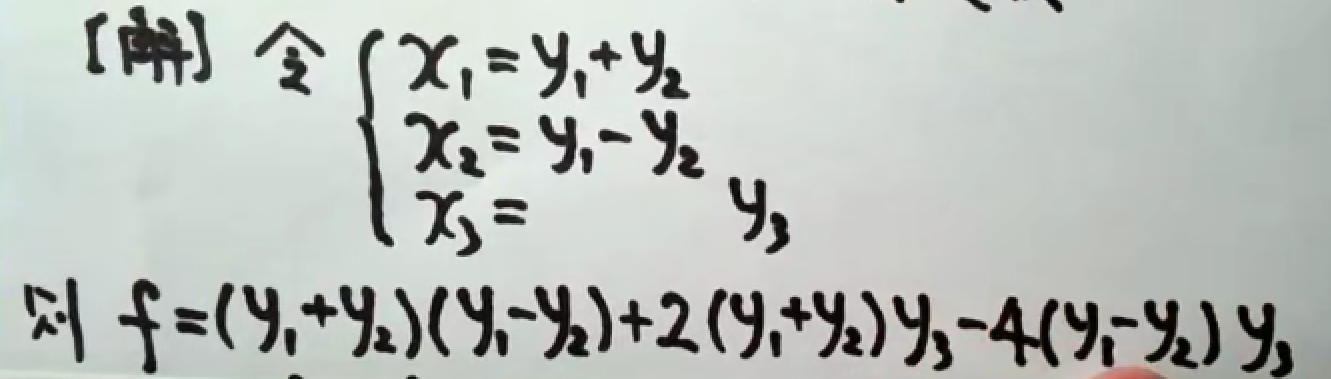

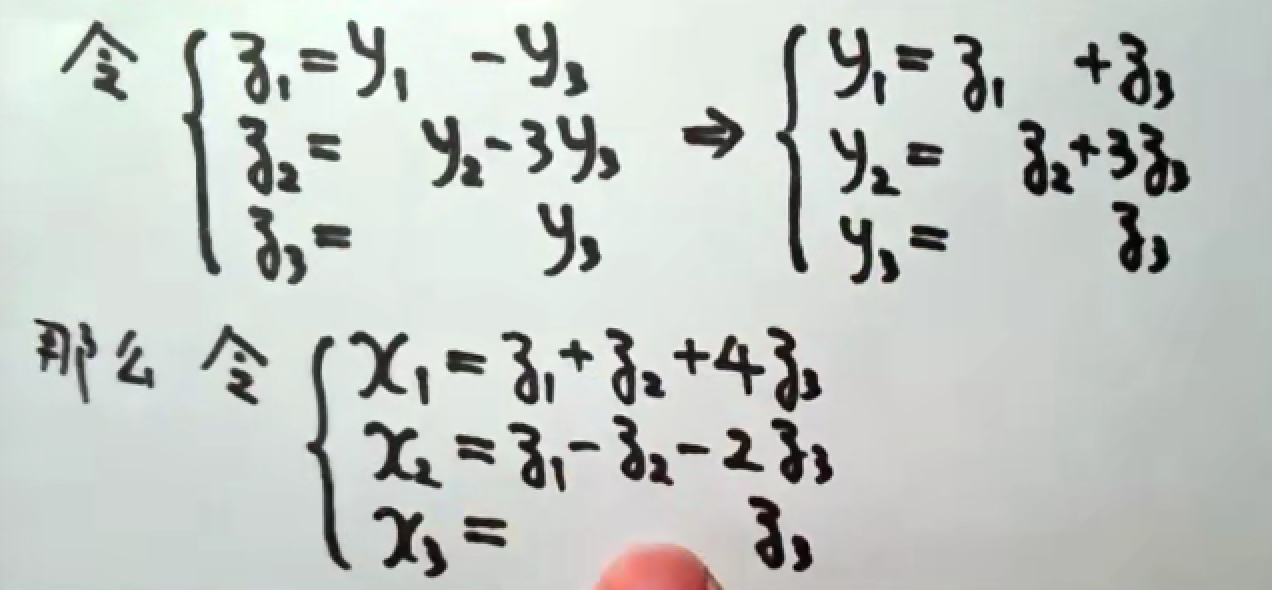

总结:先从x1开始,将带有x1项合并,凑出完全平方公式后;对x2实施同样的操作,直至所有的xn都变为平方项。最后把完全平方的项进行“换元”。
注:最后一步x=cy请看第五章坐标变换。
法2.正交变换法(重要!!)

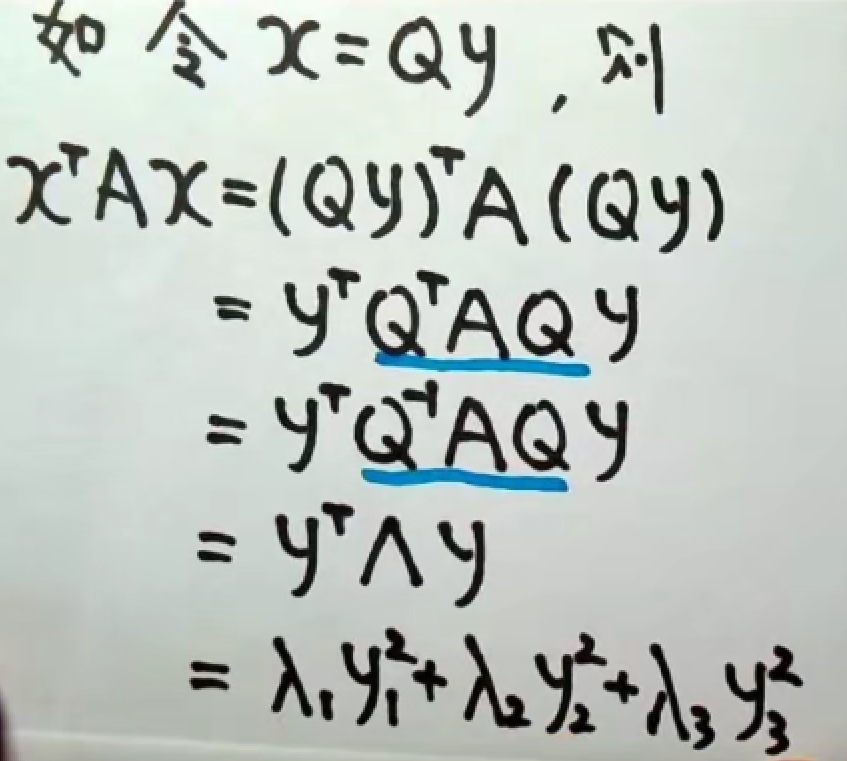
归为定理:

由上,我们把问题归结为求解A矩阵的特征值与特征向量。
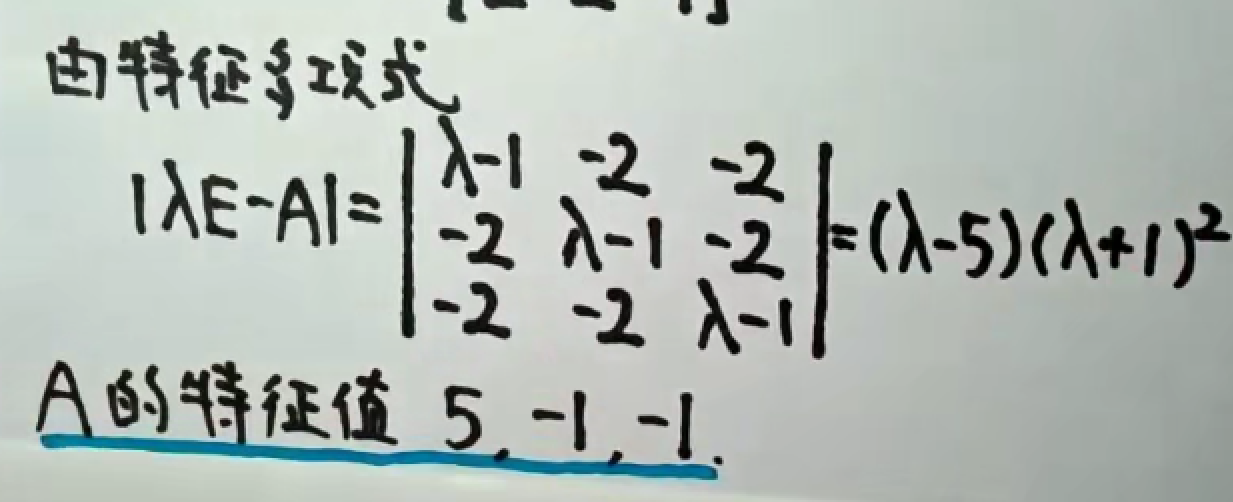
例1

求解特征值
求解特征向量

tips:实对称矩阵不同特征值的特征向量必正交。若特征值相同的情况,特征向量不一定正交。如果是正交的情况(内积为0),则不必做施密特正交化;如果特征向量不正交,则需要做施密特正交化。


单位化
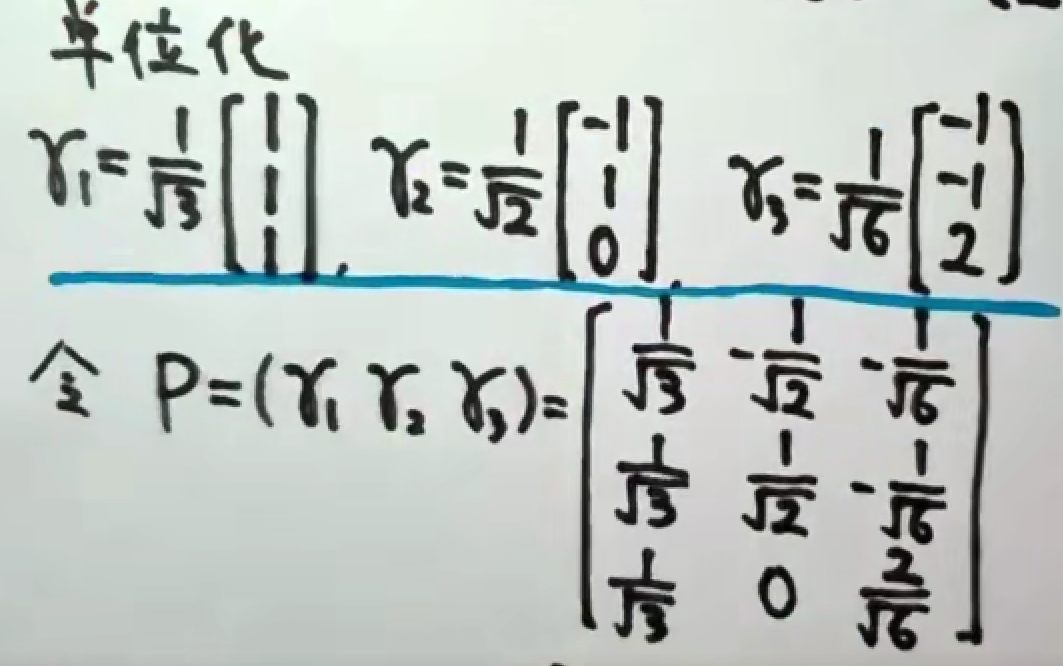
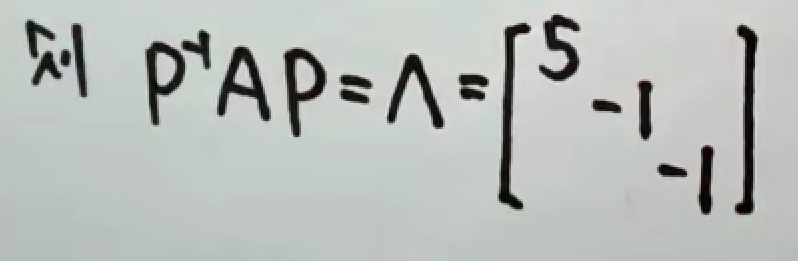
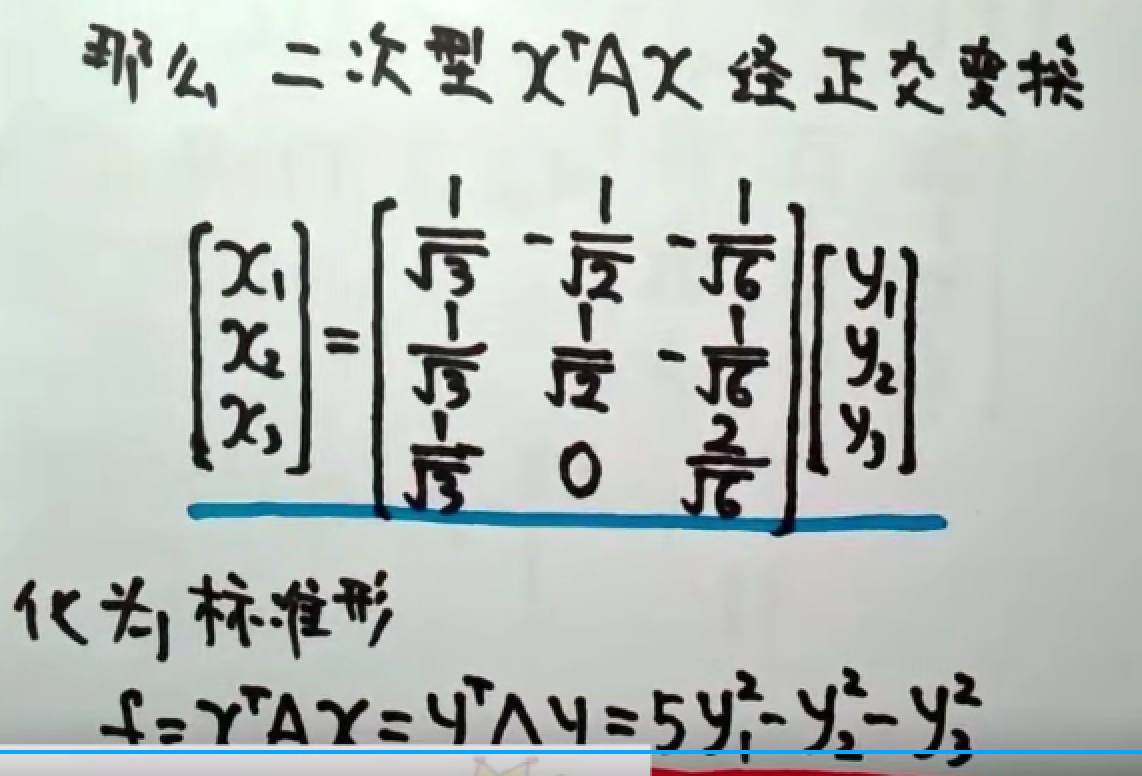
总结:
3.2.2 标准型to规范型

例题
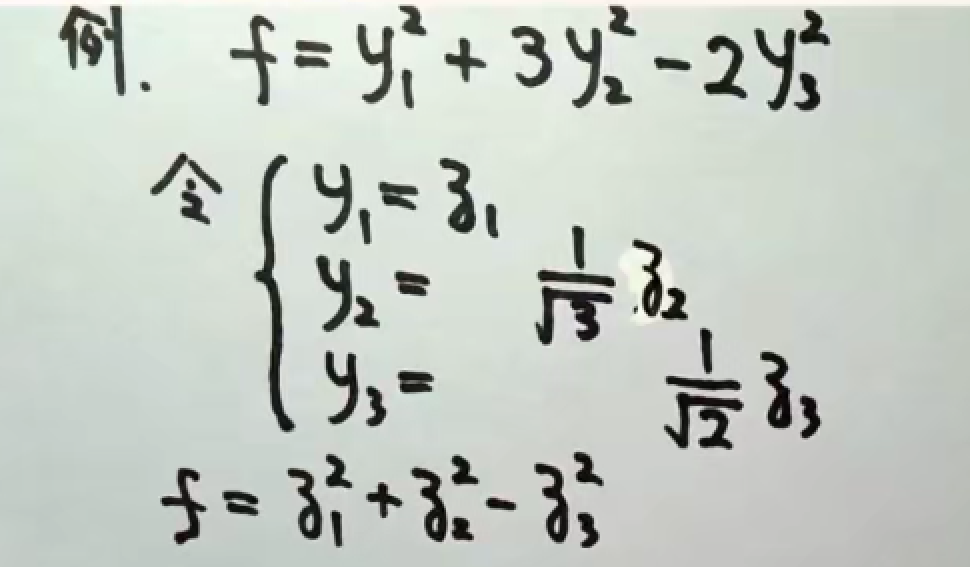
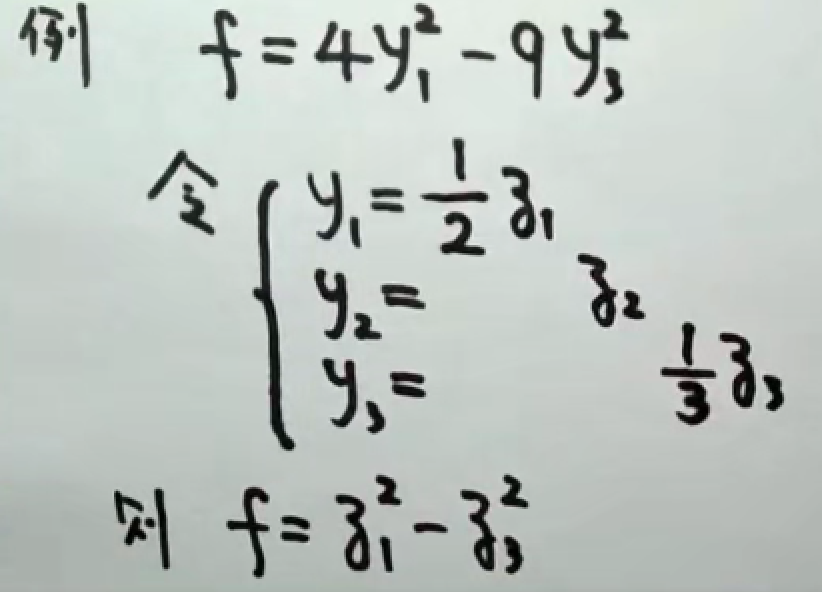
凑出系数即可。
4. 惯性指数与惯性定理
4.1 惯性指数
惯性指数分为正惯性指数与负惯性指数。

计算方式很容易,正惯性指数就是正系数个数,负惯性指数就是负系数个数,仅针对标准型而言。
4.2 惯性定理

用人话说,就是二次型经过不同的坐标变换,得到的系数可能不同,但惯性指数是确定的。即正的有几项,负的有几项,是唯一确定的。
即,标准型可能不同,但规范型一定是唯一的。
几何角度理解惯性定理:
例如,我们取了平面上一个中心在原点的一个椭圆 经过适当的线性替换, 这个椭圆一定可以化为
的形式
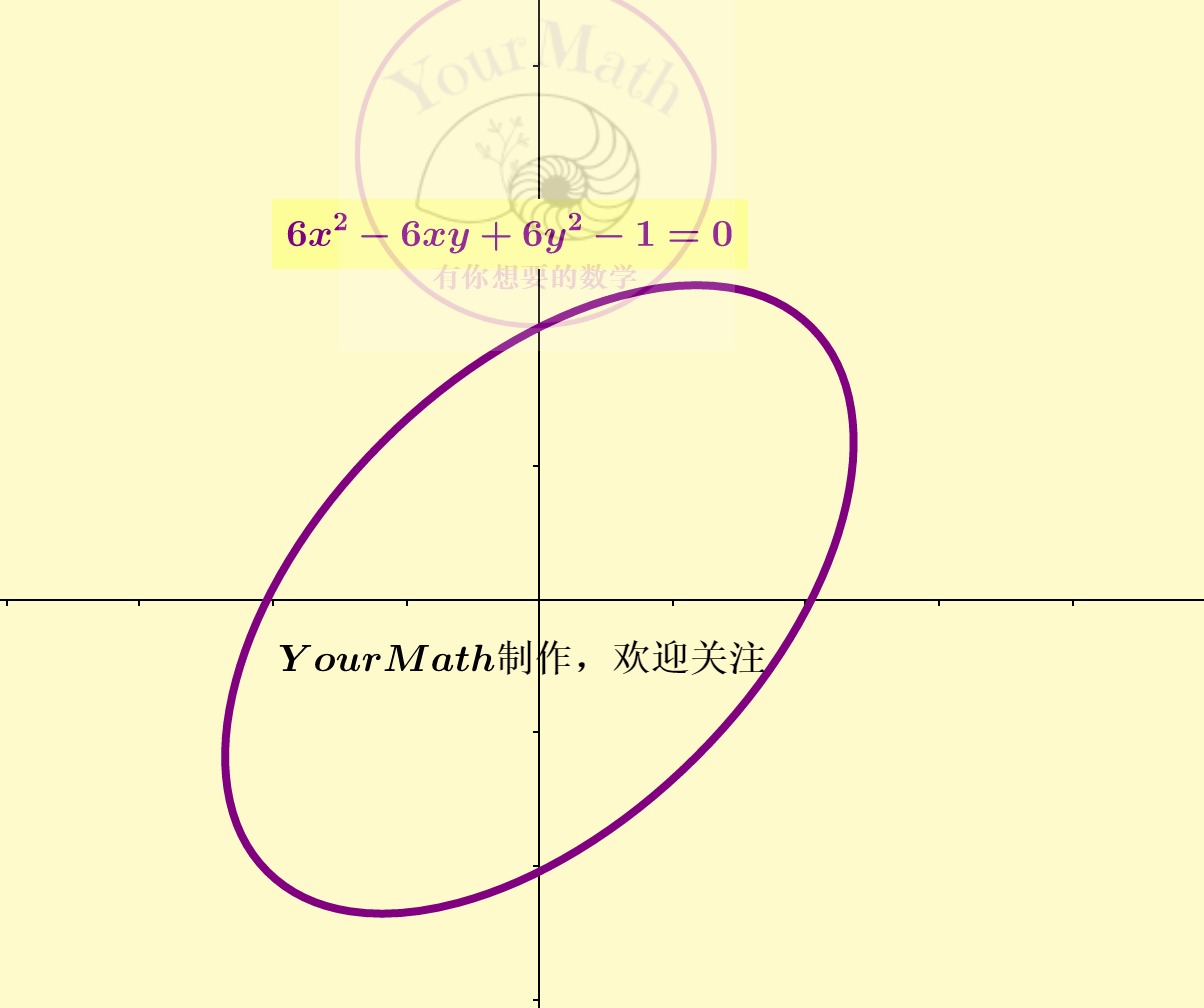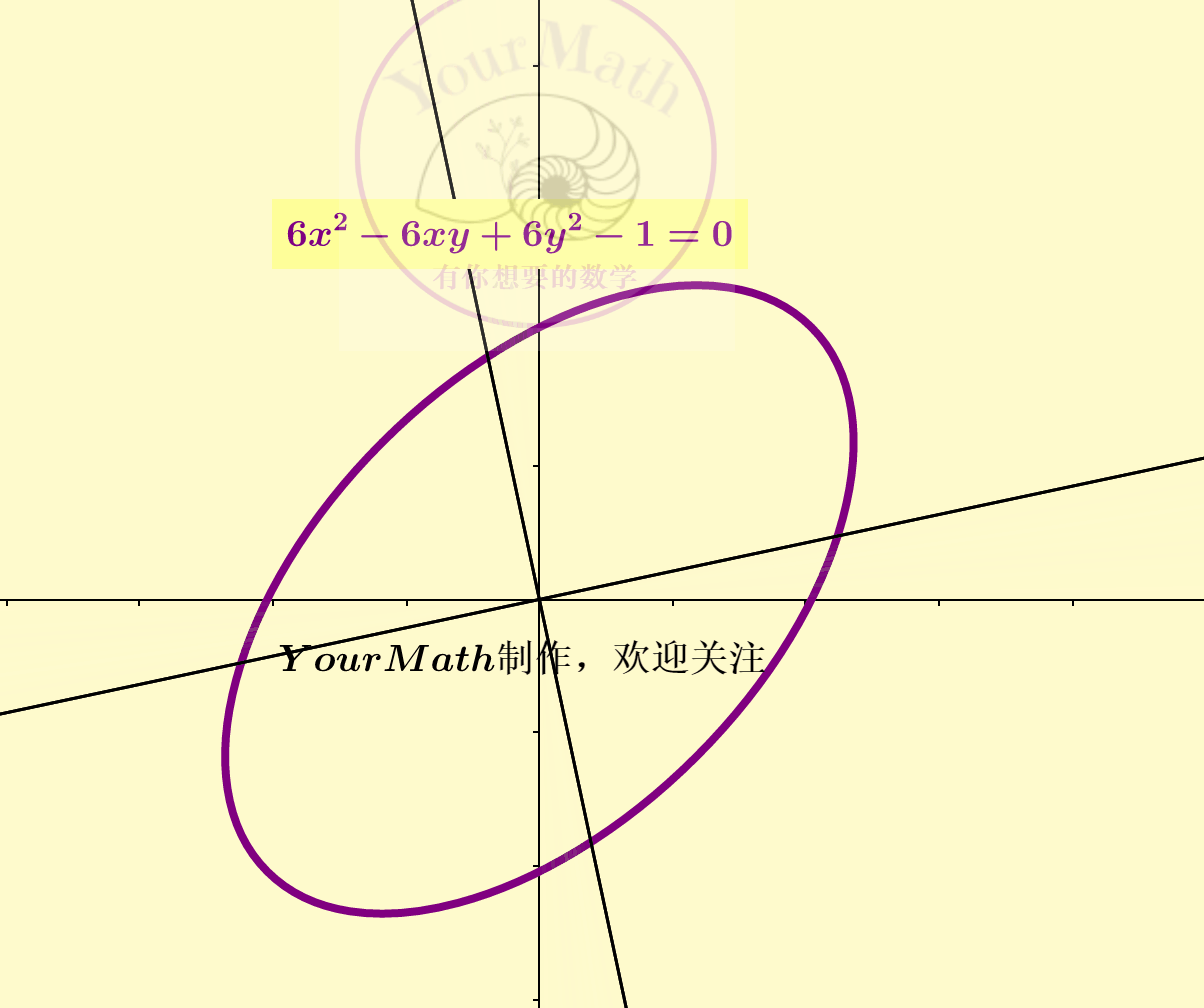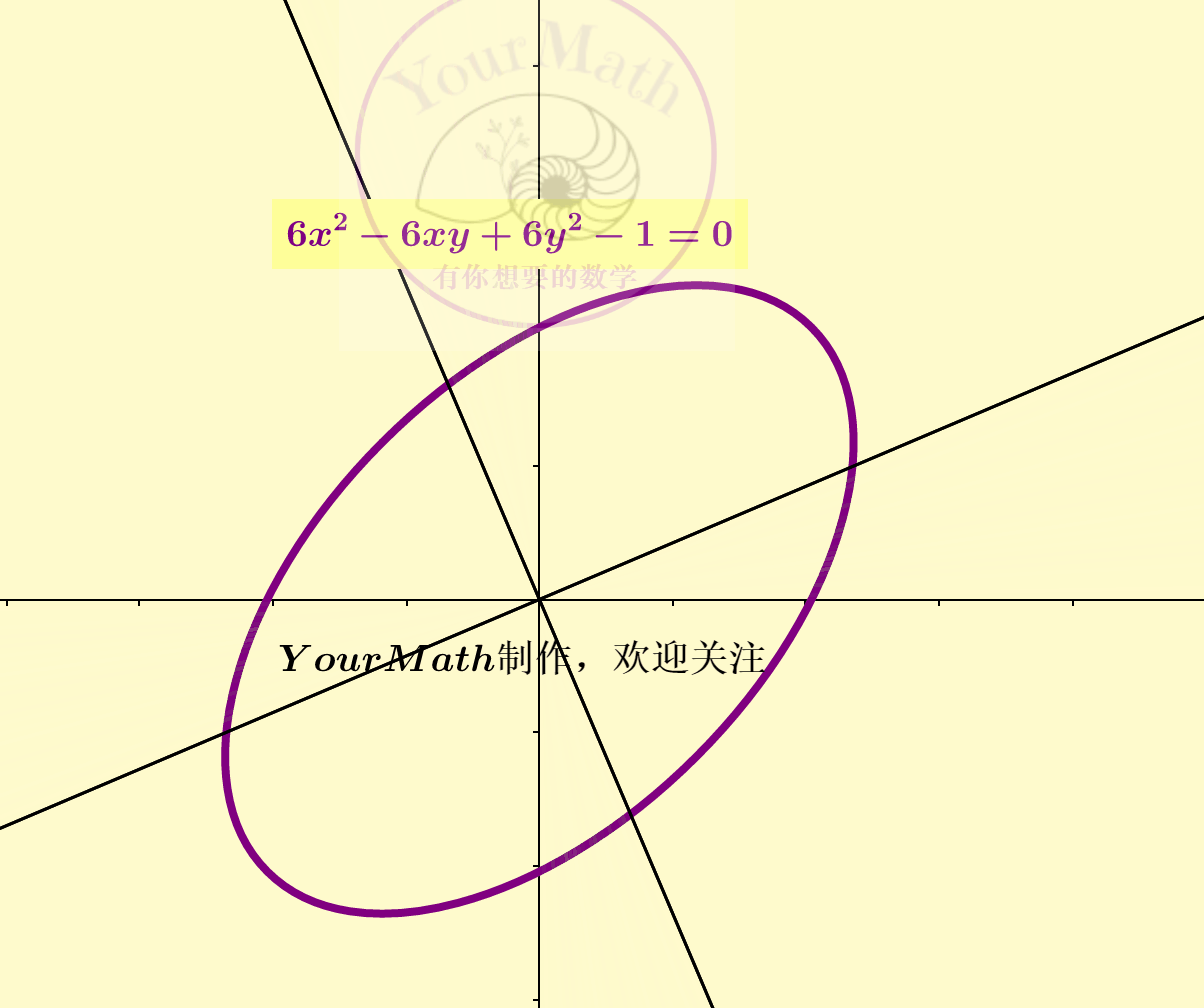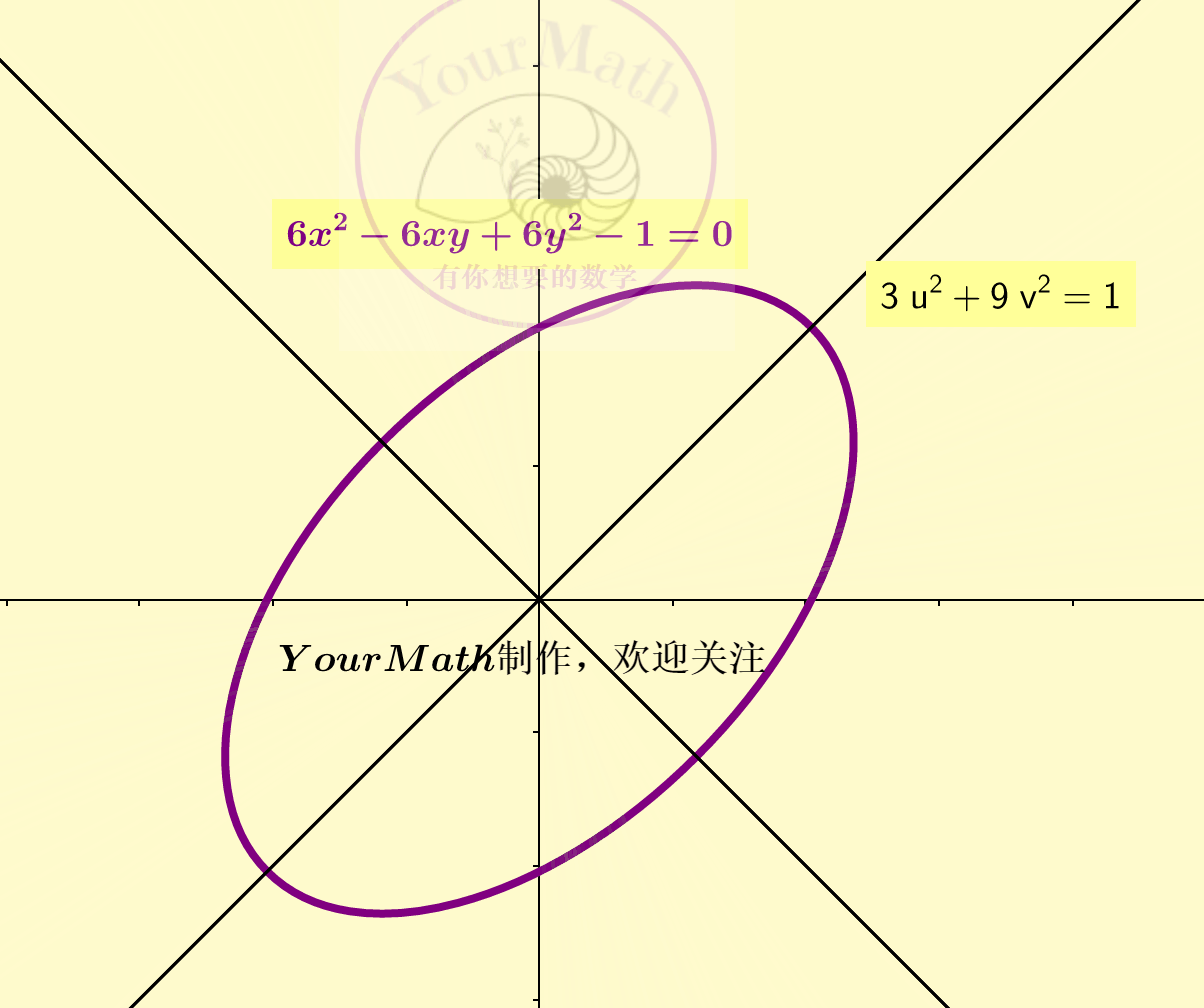
从而这个椭圆的规范形为。
注意二次型的标准形不是唯一的,它与所选的坐标变换有关。由之前介绍的标准二次方程在一般坐标系下的图像可知,不论选取哪一个坐标系变为了标准形,椭圆的方程一定为
其中
这时候,再令坐标轴单位做一下伸缩变换,就可以使原图像的方程变为
也就说,一个椭圆的规范形是唯一的。
线性角度理解惯性定理:
因为坐标系的替换也可以理解为一个线性变换。因此,每一个线性替换可以理解为将原来的二次曲线,通过线性替换矩阵所对应的线性变换,变为了一个新的二次曲线。下图为一个椭圆经过不同的线性变换后的图像:
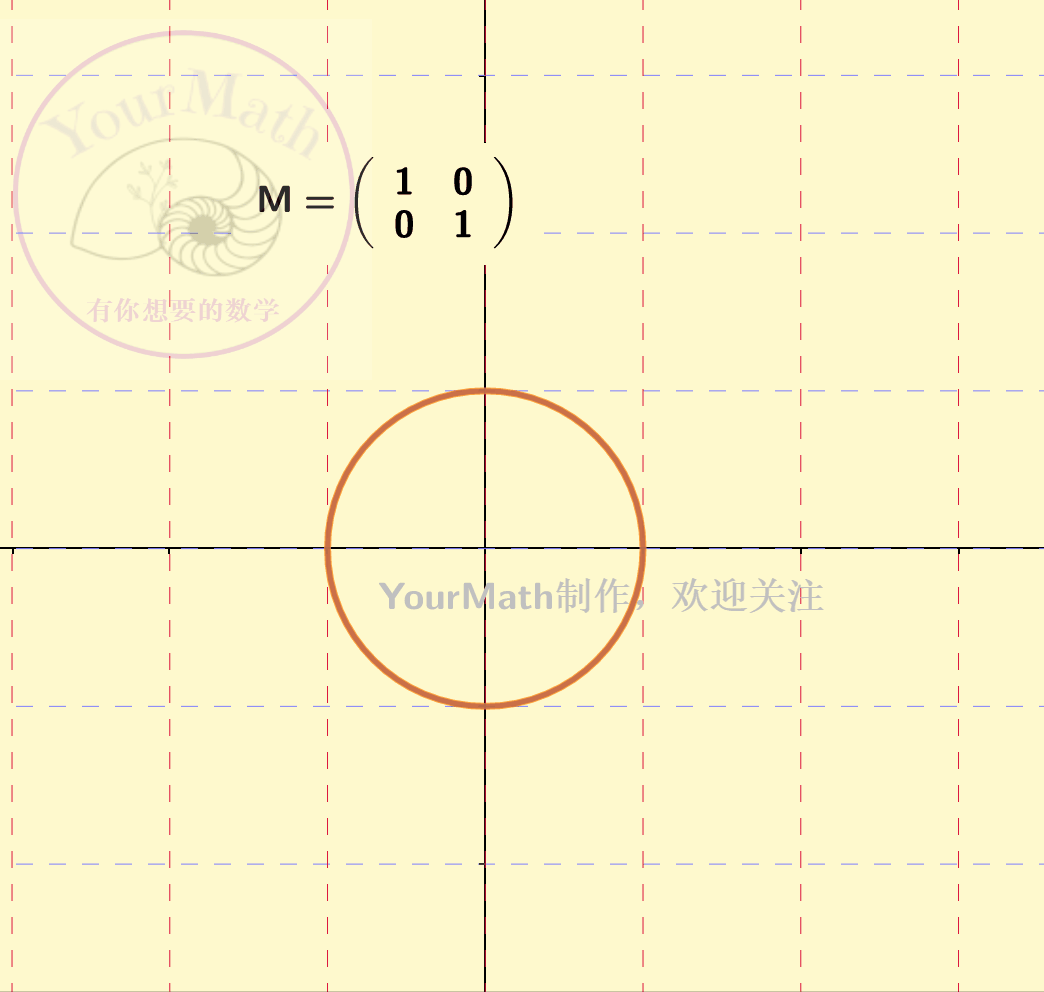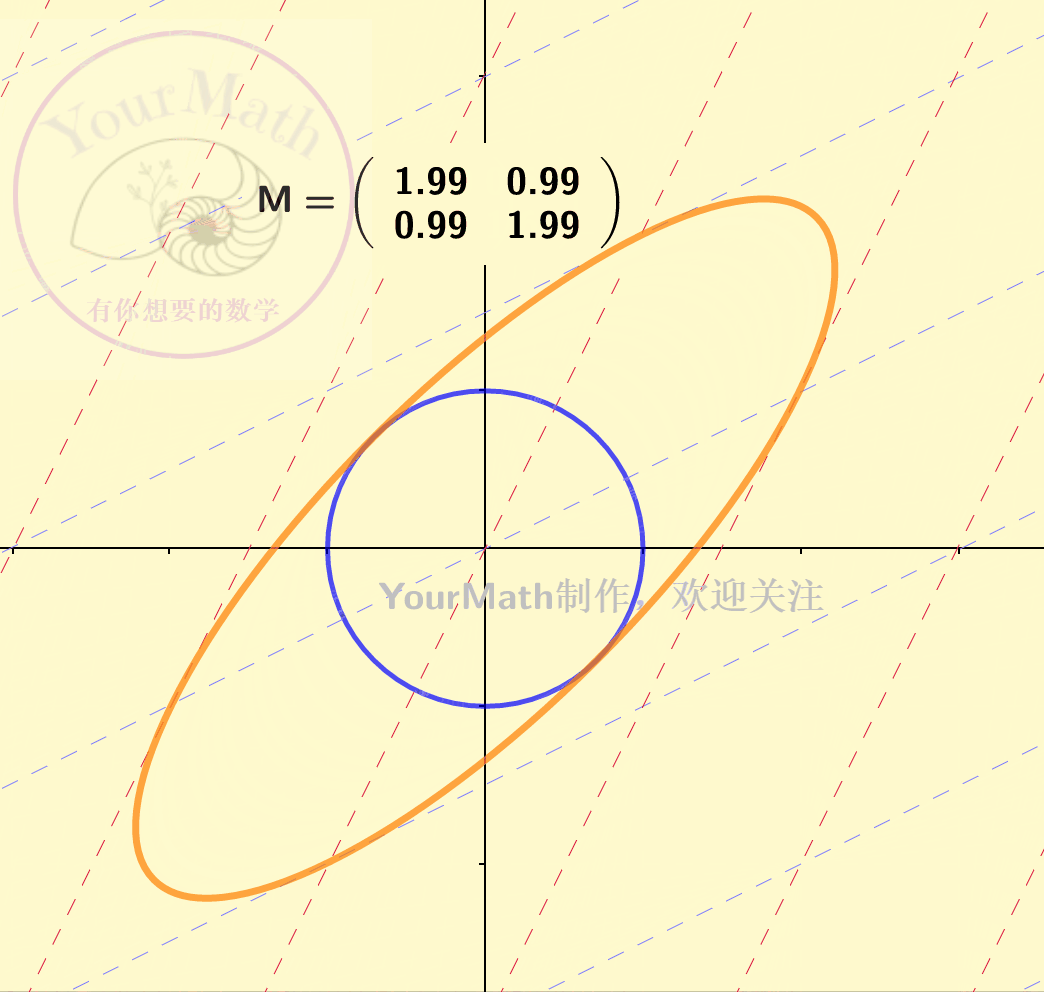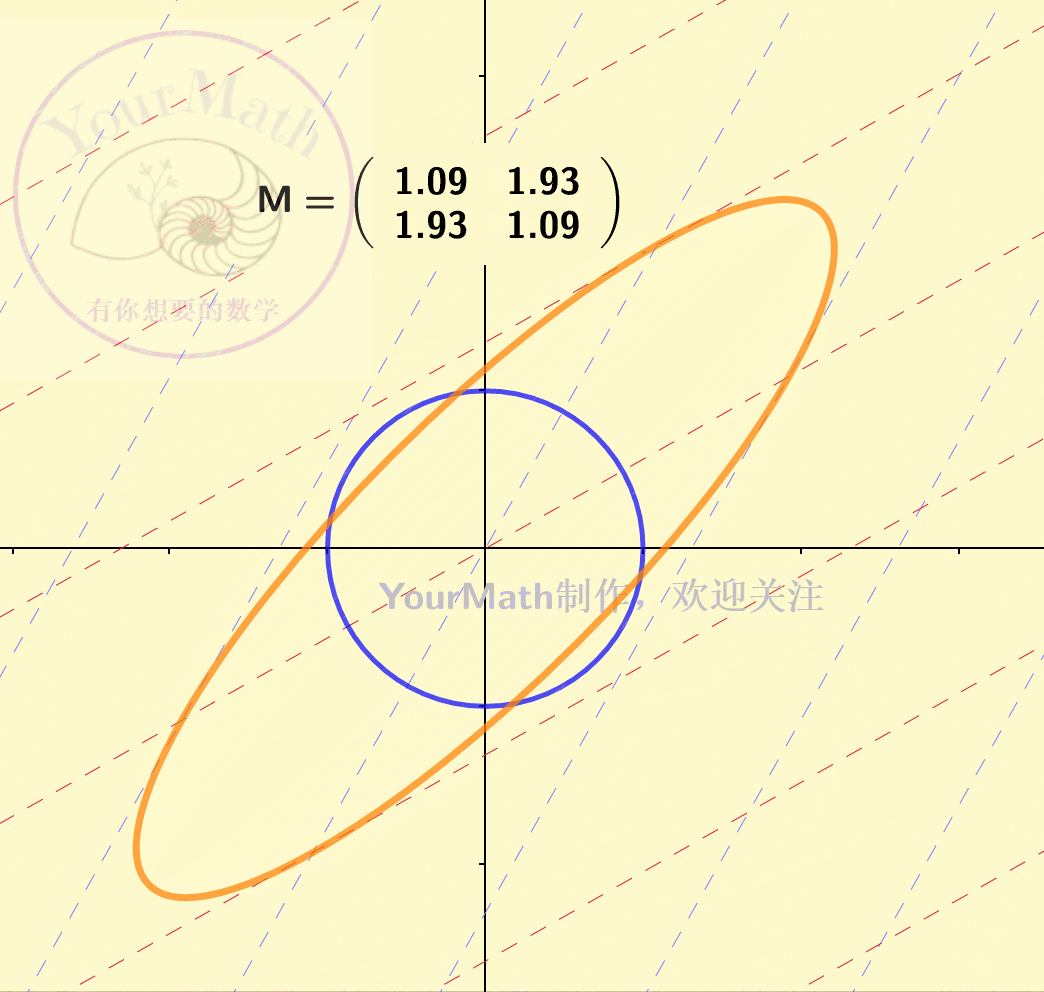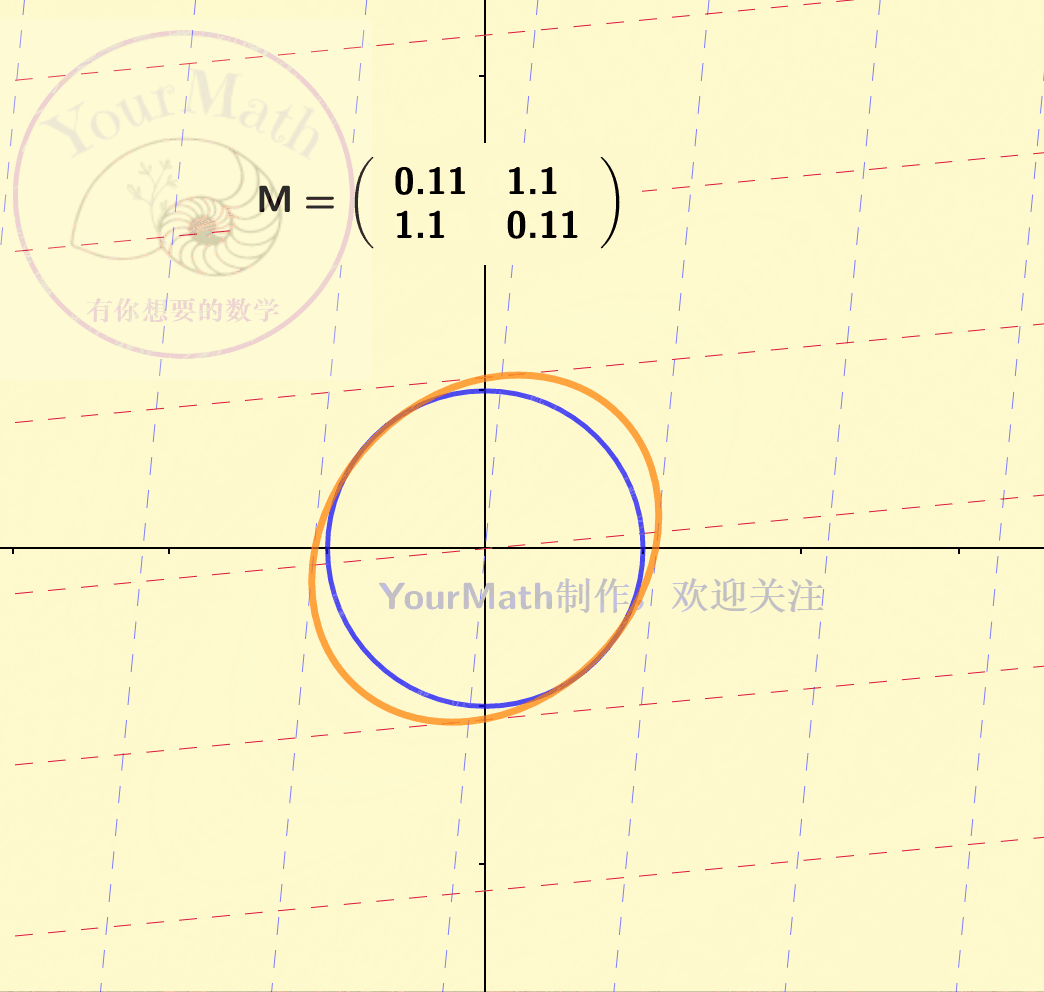
下图为一个双曲线经过不同的线性变换后的图像:
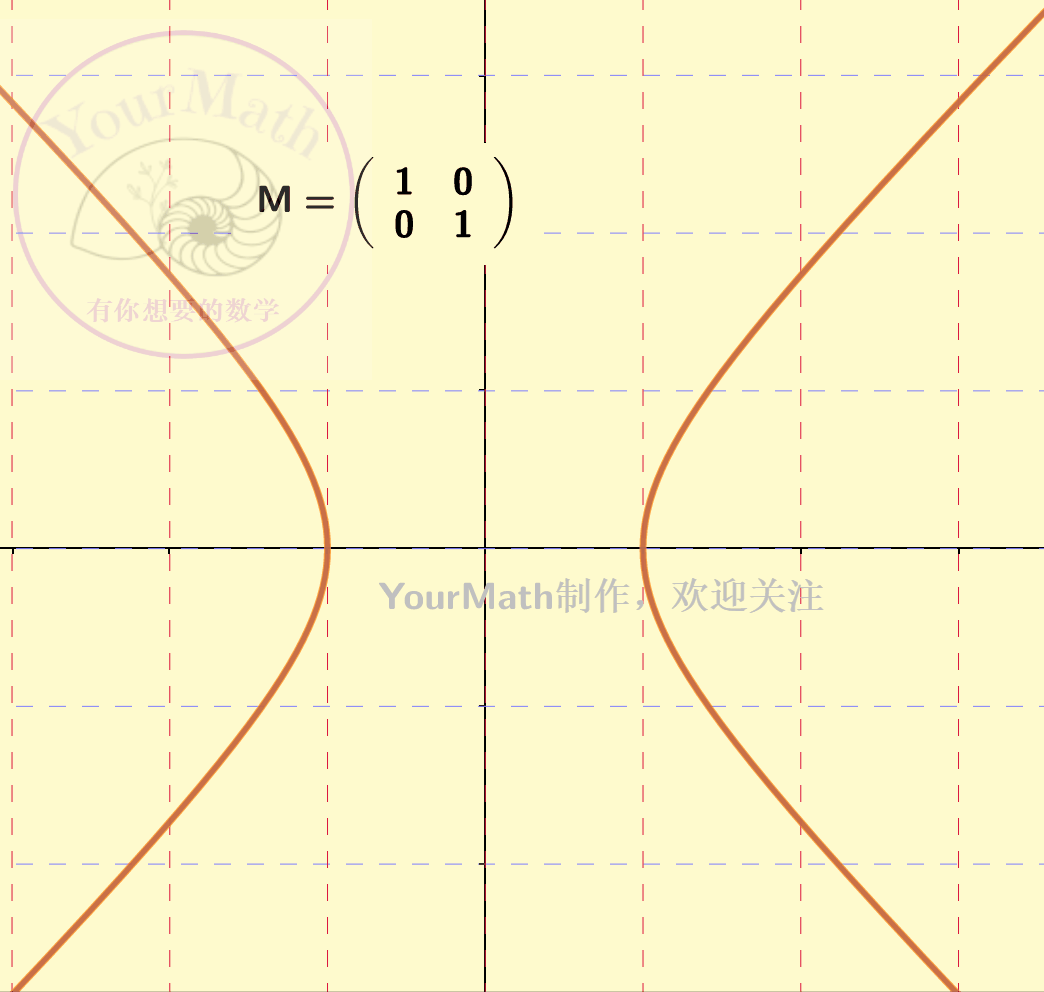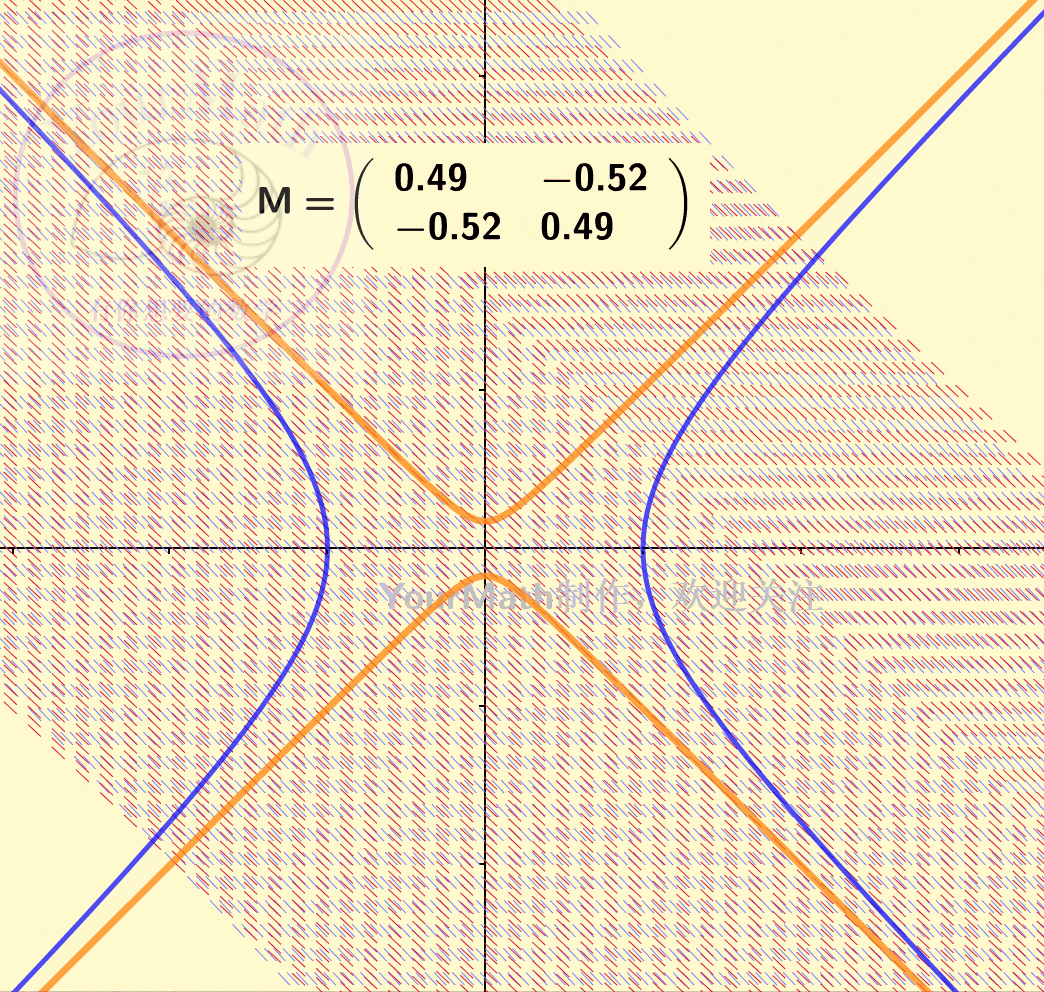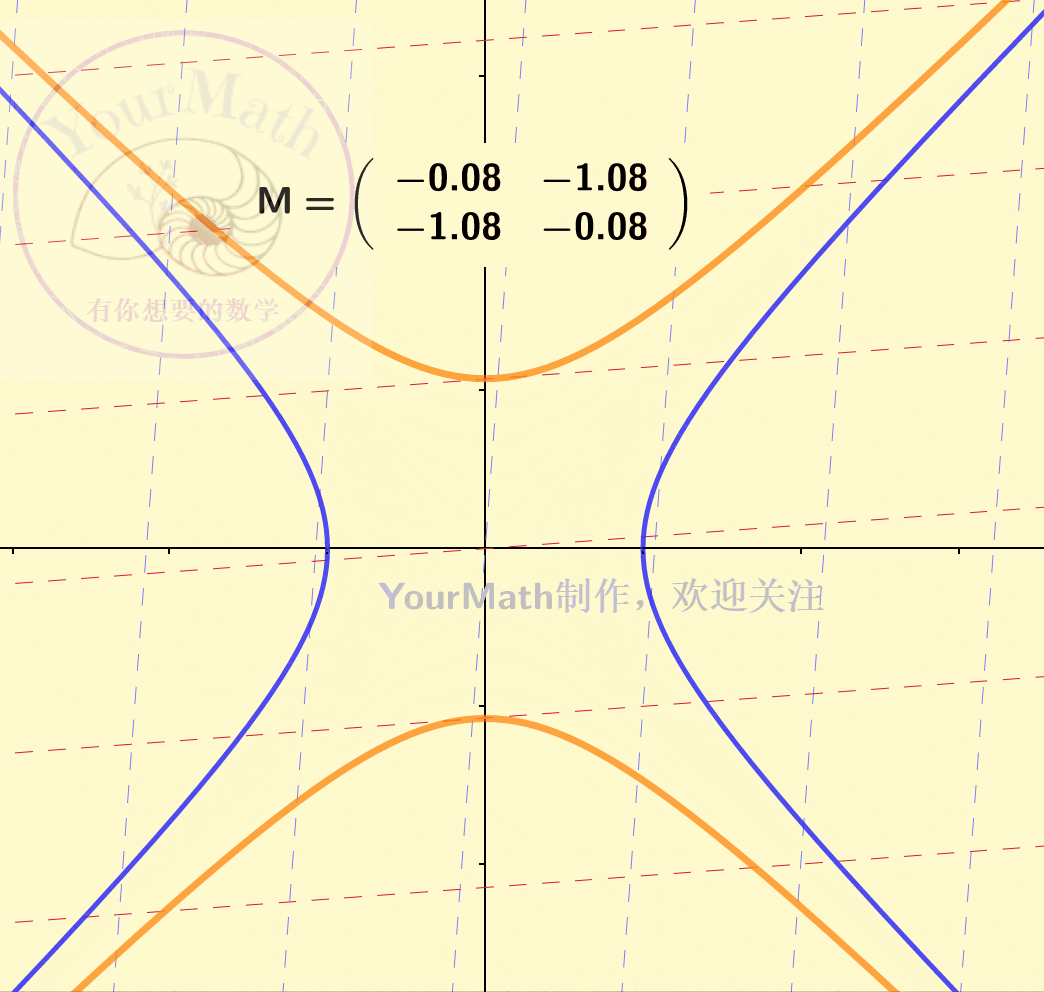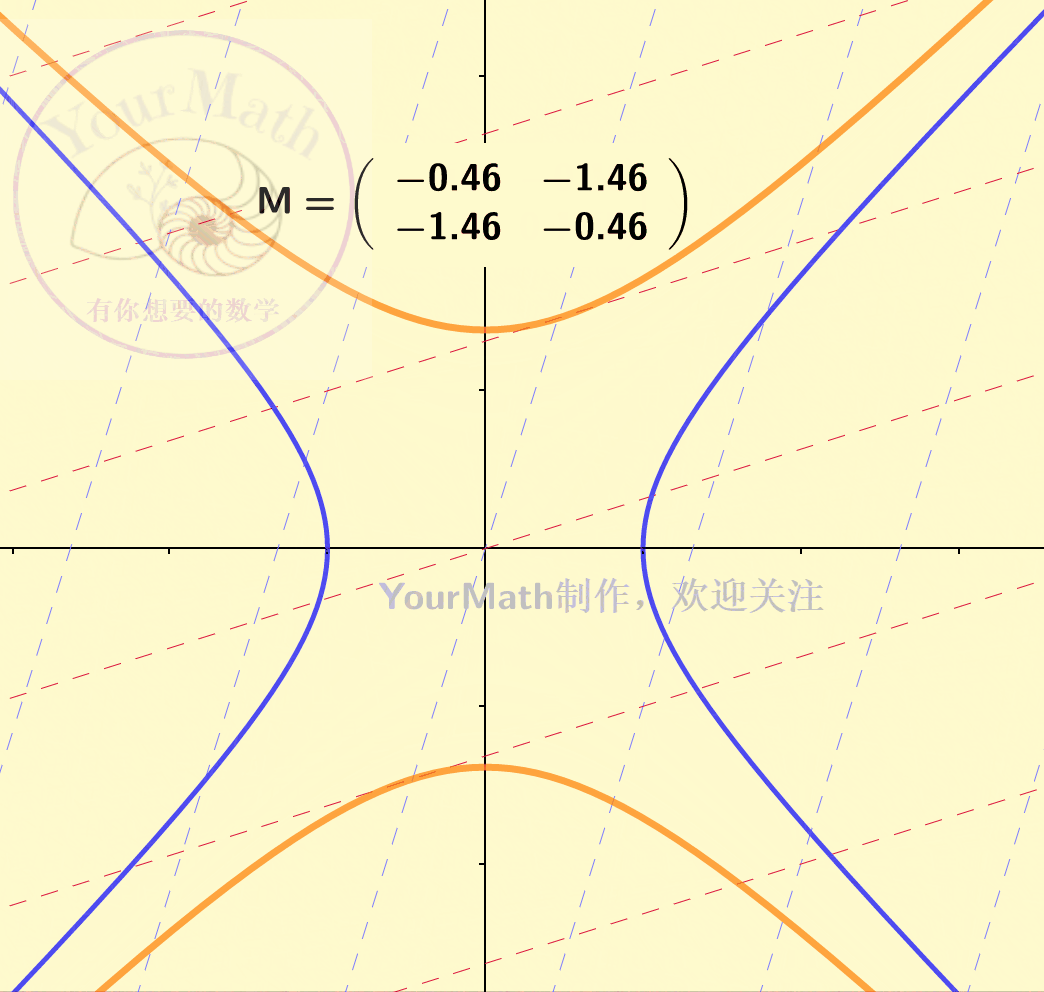
惯性定理,可以理解为任何一个椭圆 / 椭球 / 双曲线…. 在经过一个可逆的线性变换之后依然是一个椭圆 / 椭球 / 双曲线…。
5.坐标变换
5.1 定义

前提:C矩阵可逆
5.2 示例
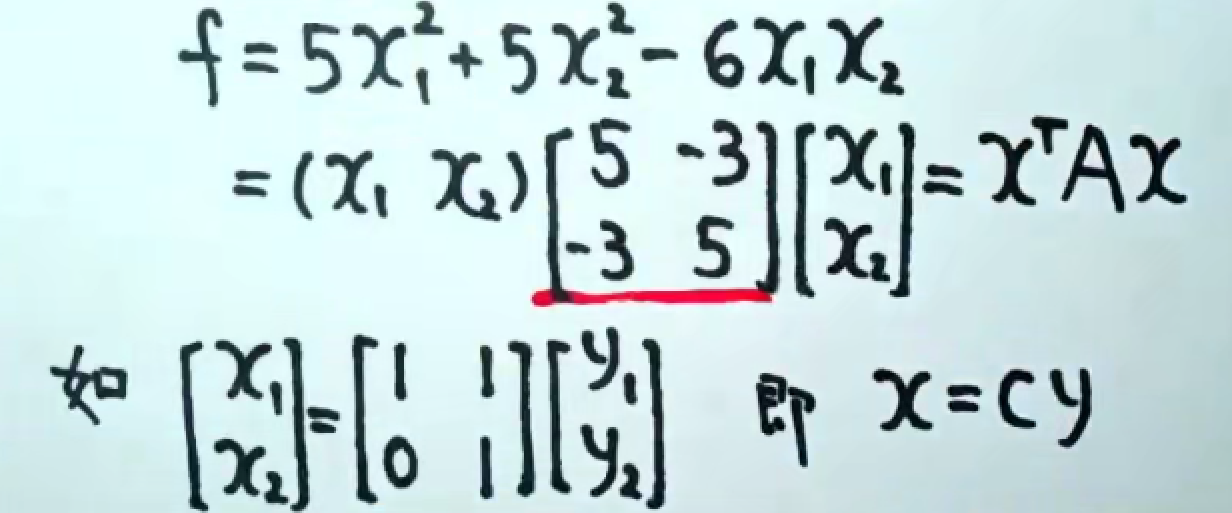

5.3 合同
定义

矩阵等价、矩阵相似、二次型合同比较
矩阵等价:;同型矩阵而言;一般与初等变换有关;秩是矩阵等价的不变量,两同型矩阵相似的本质是秩相似;
矩阵相似:;针对方阵而言;秩相等为必要条件;本质是二者有相等的不变因子;可看作是同一线性变换在不同基下的矩阵;矩阵相似必等价,但等价不一定相似;
矩阵合同:;针对方阵而言;秩相等为必要条件;本质是秩相等且正惯性指数相等,即标准型相同;可通过二次型的非退化的线性替换来理解;矩阵合同必等价,但等价不一定合同。
性质

判定

根据这个规则,可以判断矩阵是否合同。
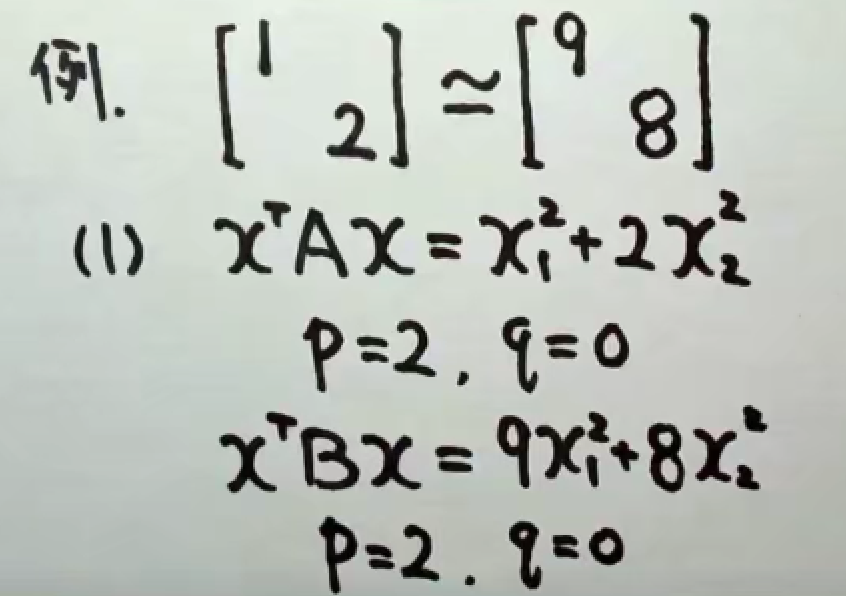

6. 正定二次型
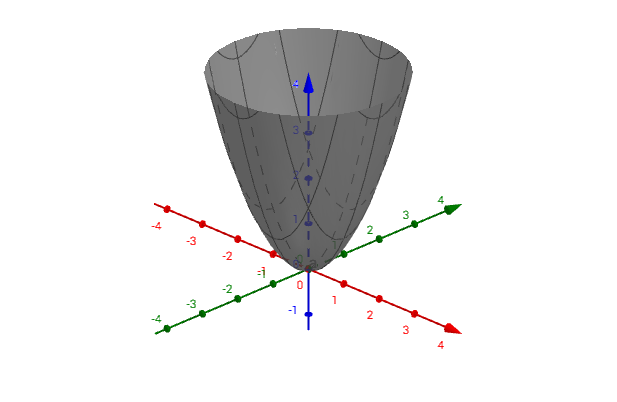
6.1 定义

从图像上看,这是正定:
6.2 定理

6.3 判定
法1:转换为标准型,通过等价条件

法2:通过必要条件
对角线上元素都要大于0。

例题


顺序主子式:方阵的k阶顺序主子式是由该方阵的前k行和k列元素组成。




7. 总结
(待续)
部分内容转自:
https://www.zhihu.com/question/38902714/answer/195435181
https://zhuanlan.zhihu.com/p/141824840
李永乐老师的线代教程
感谢!


