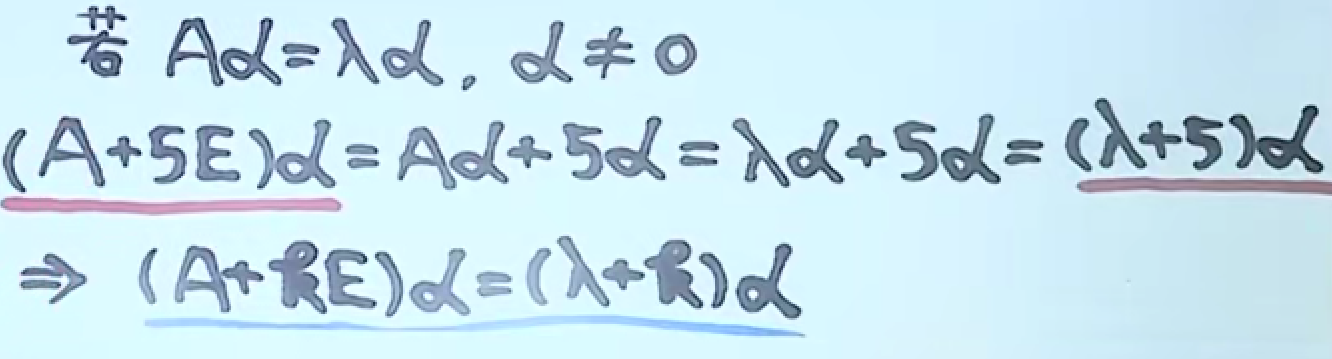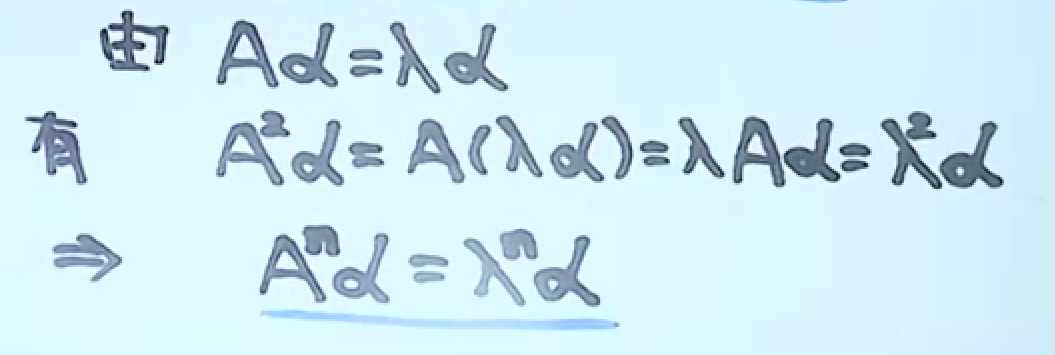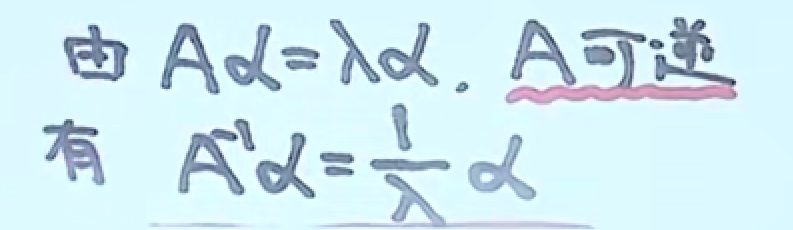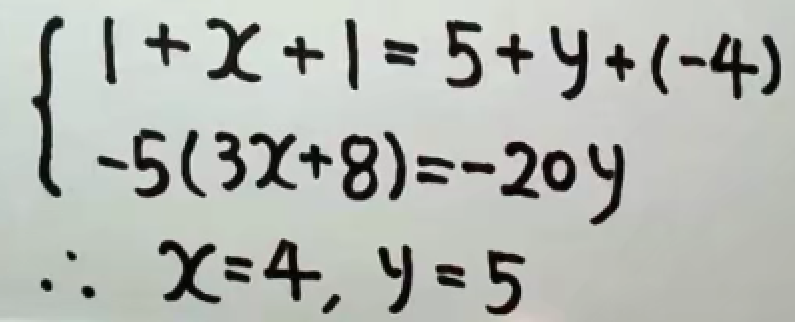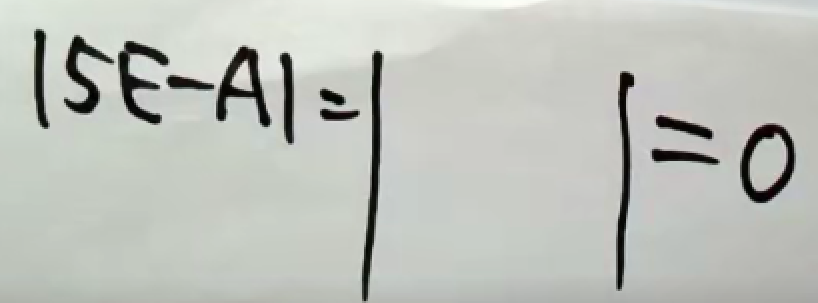快完结了,这应该是倒数第二章。这章内容是特征值与特征向量,和前面的内容还是挺不一样的。前面的内容以解方程组为目的。特征值与特征向量,其实它是有特别的用途的。
在graphics这门课里学习了图形的translate、rotate、scale操作,它们都是通过矩阵来实现的。
所以,矩阵的本质就是是空间的线性变换。
1. 特征值与特征向量
1.1 定义
首先康康定义

从感性上我们理解一下这个公式。
在这次空间变换中,矩阵将特征向量操作之后,还在它原来的直线上,且进行了缩放。而缩放的倍数,就是特征值。
1.2 定理
定理1

对角线和就是特征值和,定义为A矩阵的迹。特征值累乘就是行列式的值,由此还导出A可逆的又一个新充要条件。
定理2

1.3 求解方法
1. 定义法
定义法就是由定义出发,推导出新公式,利用这些公式直接或间接求出特征值与特征向量。
公式1
公式2
公式3
公式4
看一些例题~

2. 间接求解
将定义进行变形,可以间接的求解特征向量。
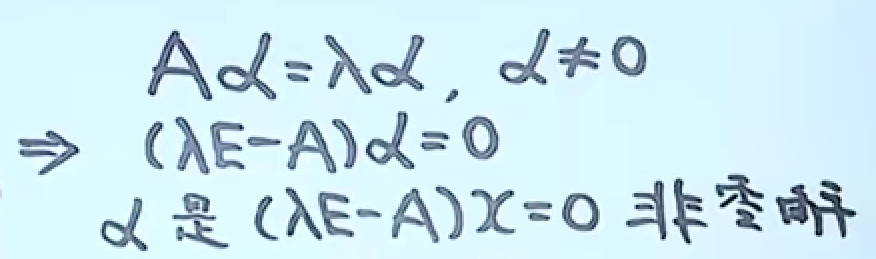
求解方法:

我们称为特征多项式。
先通过特征多项式求解出特征值(齐次方程组行列式等于0,对应非零解情况,因为特征向量不为零向量)。再对每个特征值求解出对应的特征向量。
下面看几道例题熟悉一下方法~
例1.

tips:为避免三次方程,我们需要消掉关于λ的一行或一列中非0元素,用这一行或一列展开。消去的技巧是,使用带λ的行或列加到另一行或列,如果有两行或两列的λ成比例,且能够使其他元素为0,则可以通过倍加,把这个带λ的项消去。
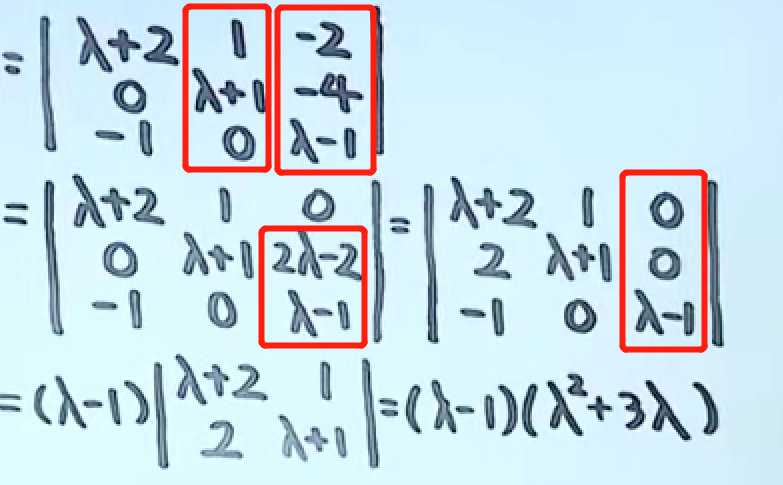
看这个栗子,第二列的1与第三列的-2可以通过倍加,把-2变为0,同时-4变为2λ-2,这时,2λ-2与λ-1呈倍数关系,又可以倍加消去,最后这一列只剩下λ-1,就用这一列展开,舒适~

对三个特征值分别求出基础解系,得到特征向量


例2




求基础解系时,不一定要化为行最简,灵活把握,计算量最小即可。
例3


重根个数与特征向量个数无必然关系,见例2与例3。这里二重根,但只有一个特征向量,例2的二重根有两个特征向量。特征向量的值小于重根个数,但没有必然的关系。
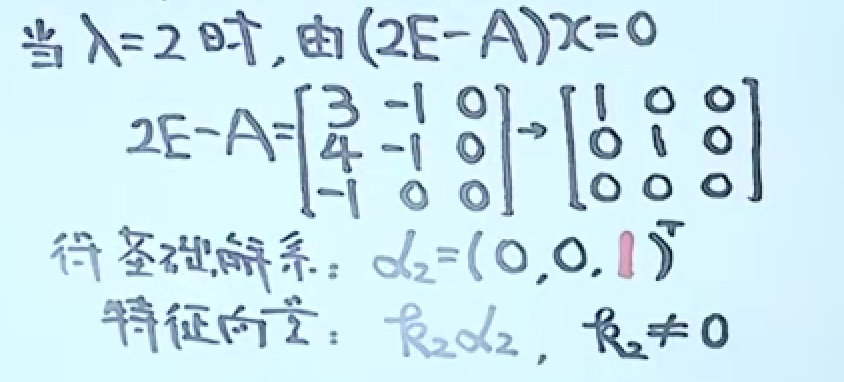
2. 相似矩阵
2.1 定义

p.s. 一个A矩阵可以和多个矩阵B、C、D….相似
2.2 基本性质
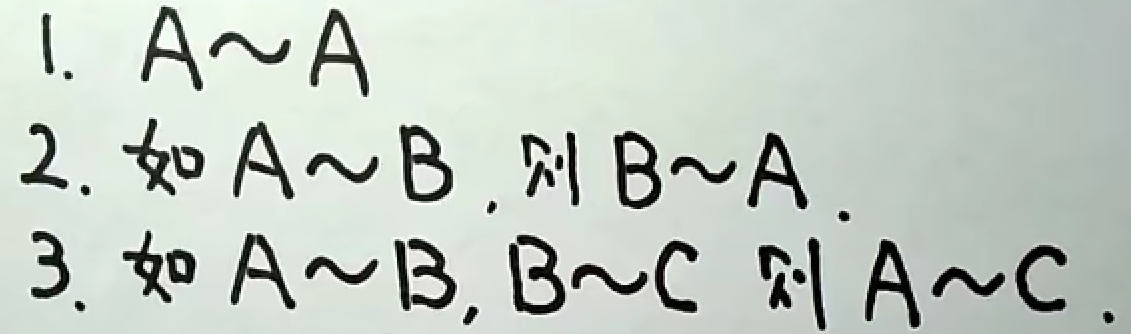
满足自反性,对称性,传递性。传递性常常考证明题,使用对角矩阵作为媒介,间接证明A与B是相似的。


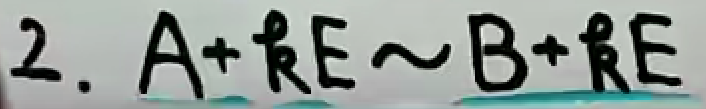


2.3 相似的必要条件
既然是必要条件,说明只有相似的情况下,这些条件才成立。而尽管这些条件全都成立,也不一定相似。
条件

可以看到,它们是不相似的,尽管特征多项式的值相同。
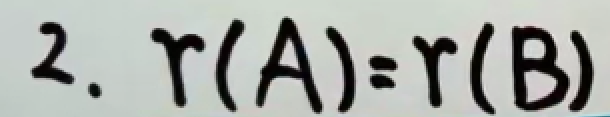
两个矩阵相似,秩相等。

两个矩阵相似,其行列式值相等。

两个矩阵相似,其迹相等。
应用
题目给出矩阵相似时,可以利用相似的必要条件构造方程组,解出参数。
例题:

法1:
法2:
利用两个矩阵的特征值相同。 法3:
3. 相似对角
3.1 定义

简单来说,就是相似矩阵的定义下,如果B矩阵是某一特定对角矩阵,则称A可以相似对角化。


如果求出来了,则其对角线的值就是A的特征值,P的分块列向量是A的特征向量。
3.2 相似对角的充要条件

3.3 相似对角的充分条件

第一条公式补充:如果特征值有重根,则要讨论重根对应的基础解系的个数。如果基础解系的个数等于重根数,则也满足。
3.4 判断是否能相似对角化
引例

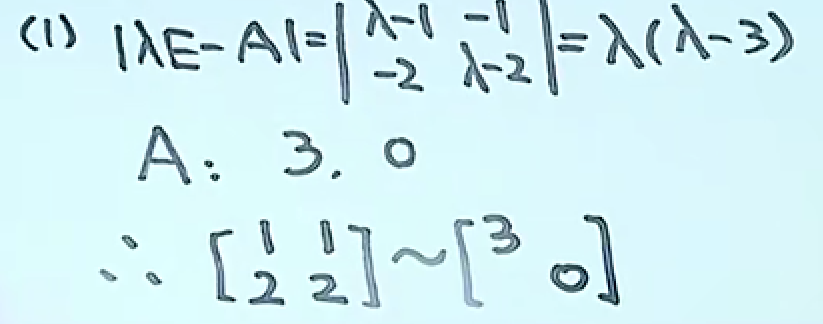
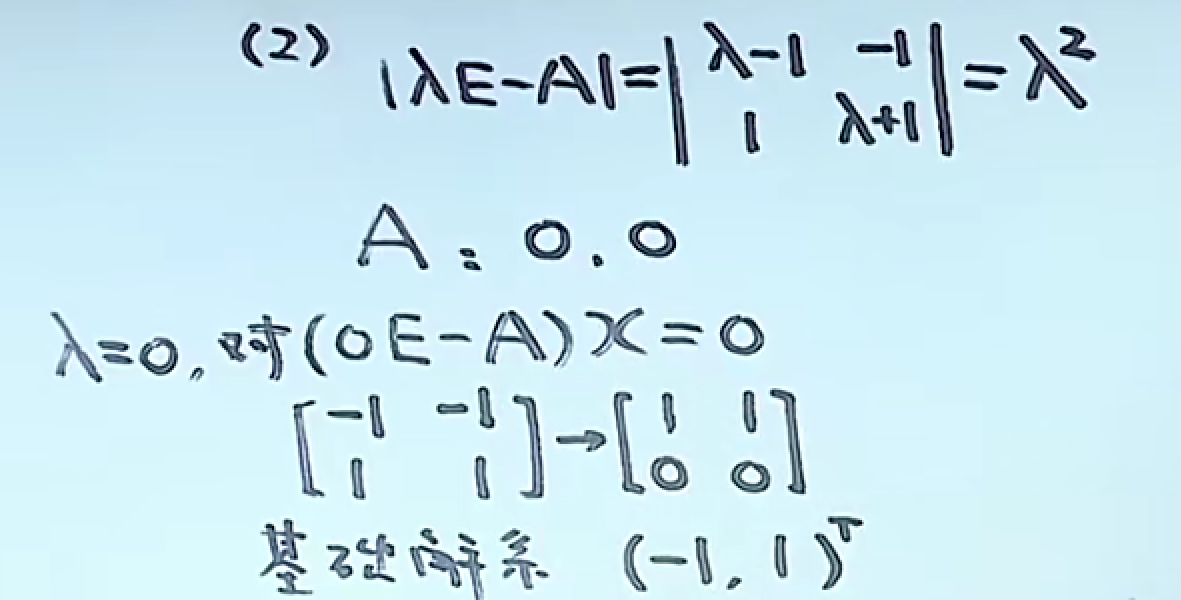


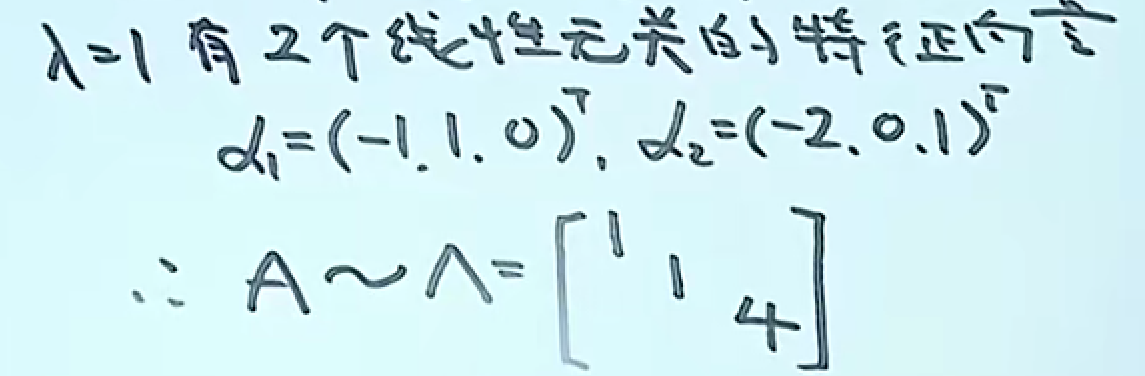
第四小题 对称矩阵一定能相似对角化(充分条件2)
方法论
找出特征值,如果个数有n个,则可以相似对角化。如果小于n,则对重根进行检验。如果重根对应的基础解系个数小于重根数,则不可相似对角化。
3.5 定理
定理1

推论:

定理2

定理3

应用
例1
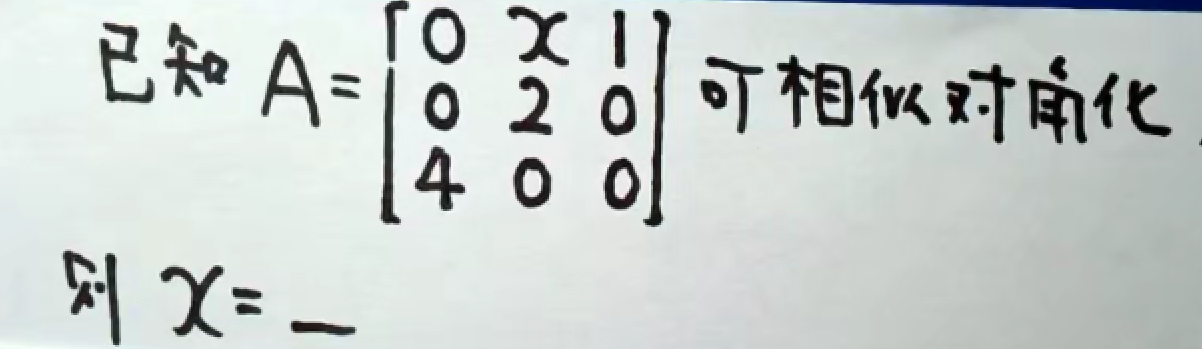

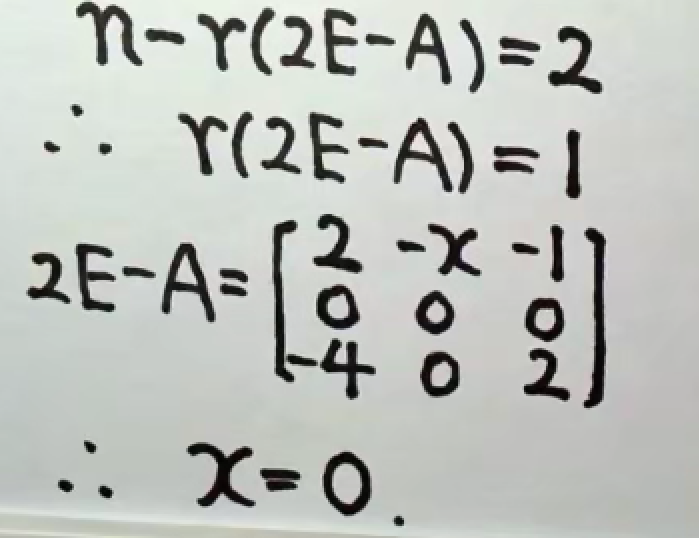
例2





例3




4. 实对称矩阵
4.1 定义
如果有n阶矩阵A,其矩阵的元素都为实数,且矩阵A的转置等于其本身(aij=aji),(i,j为元素的脚标),则称A为实对称矩阵。
4.2 定理
定理1

矩阵的特征值有可能是虚数
定理2

区别于一般的矩阵,一般的矩阵特征值不同,对应的特征向量线性无关。而实对称矩阵不同的特征值,对应的特征向量是正交的。正交是线性无关中的一个极端情况。
定理3

实对称矩阵一定可以相似对角化。实对称矩阵一定与对角矩阵相似。
例题
例1


例2



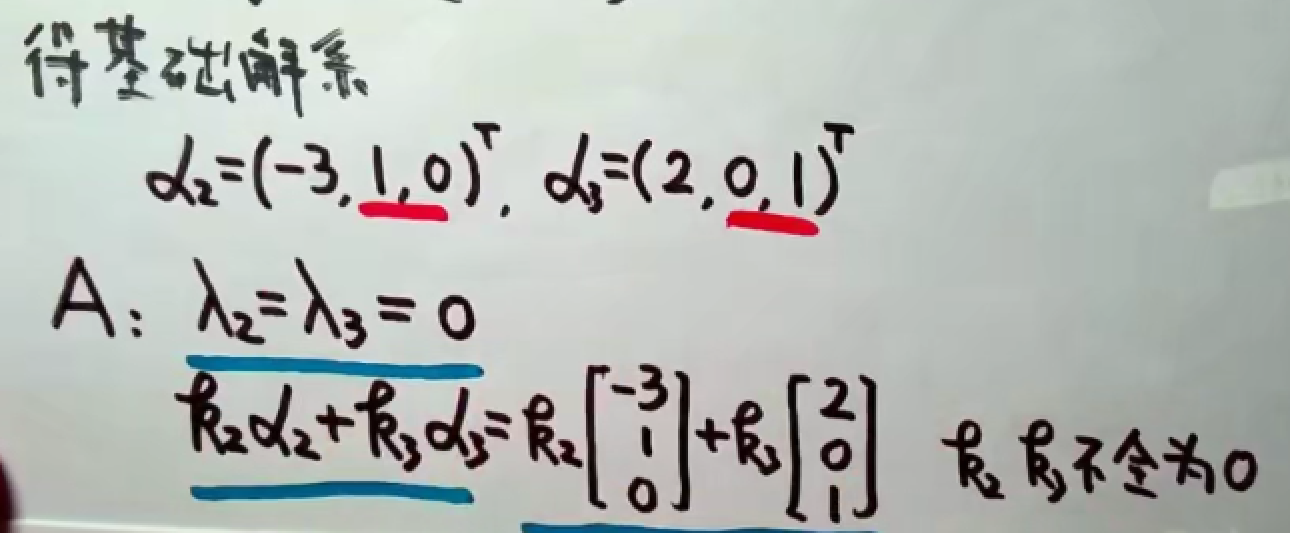
相似对角化的方法


与之前求特征向量不同的是,这里求出的特征向量如果不正交,则需要用施密特正交化将其变形。
5. 总结
(待续)