0. Intro
写在前面
本文大部分基于: https://charlesliuyx.github.io/2017/10/06/%E3%80%90%E7%9B%B4%E8%A7%82%E8%AF%A6%E8%A7%A3%E3%80%91%E7%BA%BF%E6%80%A7%E4%BB%A3%E6%95%B0%E7%9A%84%E6%9C%AC%E8%B4%A8/,与视频线性代数的本质,感谢原作者!
这篇文章将只停留在数值运算和公式的线性代数推进到可视化几何直观(Visual Geometric Intuition),致敬 3B1B 的系列视频,动图也都来自于视频。内容涉及到基变换,叉积,逆矩阵,点积,特征向量与特征值。每一章节都有一句经典的名言,非常有启发性
在笔记开始之前,想象学习一个事物(概念)的场景:我们需要学习正弦函数,$\sin (x)$,非常不幸的是,你遇到了一本相当装逼的教材,它告诉你,正弦函数是这样的:
的确很厉害的样子,并且,计算器就是这样算 $\sin (x)$,知道了这个的确 “挺酷的”。对你来说,你的作业可能就是回家把 $x= \frac{\pi}{6}$ 带到公式里面,发现,好神奇!竟然越算越接近0.5。
再假设一个场景,接下来,物理课,正弦函数随处可见,下图场景中,其他人能快速的大概估计出这个值是0.7。而刚 “学过” 正弦函数的你,内心戏可能是这样的:这些人忒 diao 了吧?你莫不是在玩我?
你可能会觉得这些做物理的人脑子也太强了,我弱爆了。其实,你需要只是一个几何直观的灌输而已,这也从侧面佐证了一个好的老师(这里的好老师真的不是他本身的学术能力有多强,而在于他擅不擅长站在学习者的角度不断的修正教学方法。甚至,模拟学生的学习过程提前预知所需要的基础概念)是有多么重要。
教学不同层次的人:初学,入门,掌握,理解,都是不同的。解释的角度,方式都完全不同。更加不幸的是,为了能更加通用的用理论来描述现实生活中的规律,人类已经做了很多工作,我们常说:越通用,越抽象(越难以理解)。这对于初学者来说堪称一段噩梦
根据生物学家我们知道,人对具体的事物(动画>图形>数字>未建立直观理解的文字)更敏感,记忆速度更快。这篇笔记的对象 3B1B 团队生产的内容目的就是从为了帮助人们建立直观概念的角度来教学。
类似于平时都是使用cpu计算矩阵,而换用gpu计算矩阵,效果更佳。cpu类似于我们的大脑,gpu类似于大脑与眼睛的组合。
1. 向量
引入一些数作为坐标是一种鲁莽的行为 ——赫尔曼 · 外尔
The introduction of numbers as coordinates is an act of violence - Hermann Weyl
1.1 向量的定义
对于向量的这个概念,大家一定并不陌生,但是这次让我们从数学,物理,计算机三个角度来看待如何定义【向量】这个概念
物理专业角度
- 向量是空间中的箭头
- 决定一个向量的是:它的长度和它所指的方向
计算机专业角度
- 向量是有序的数字列表(数组)
- 向量不过是 “列表” 一个花哨的说法
- 向量的维度等于 “列表” 的长度
数学专业角度
从数学来说,它的本质就是通用和抽象,所以,数学家希望概括这两种观点
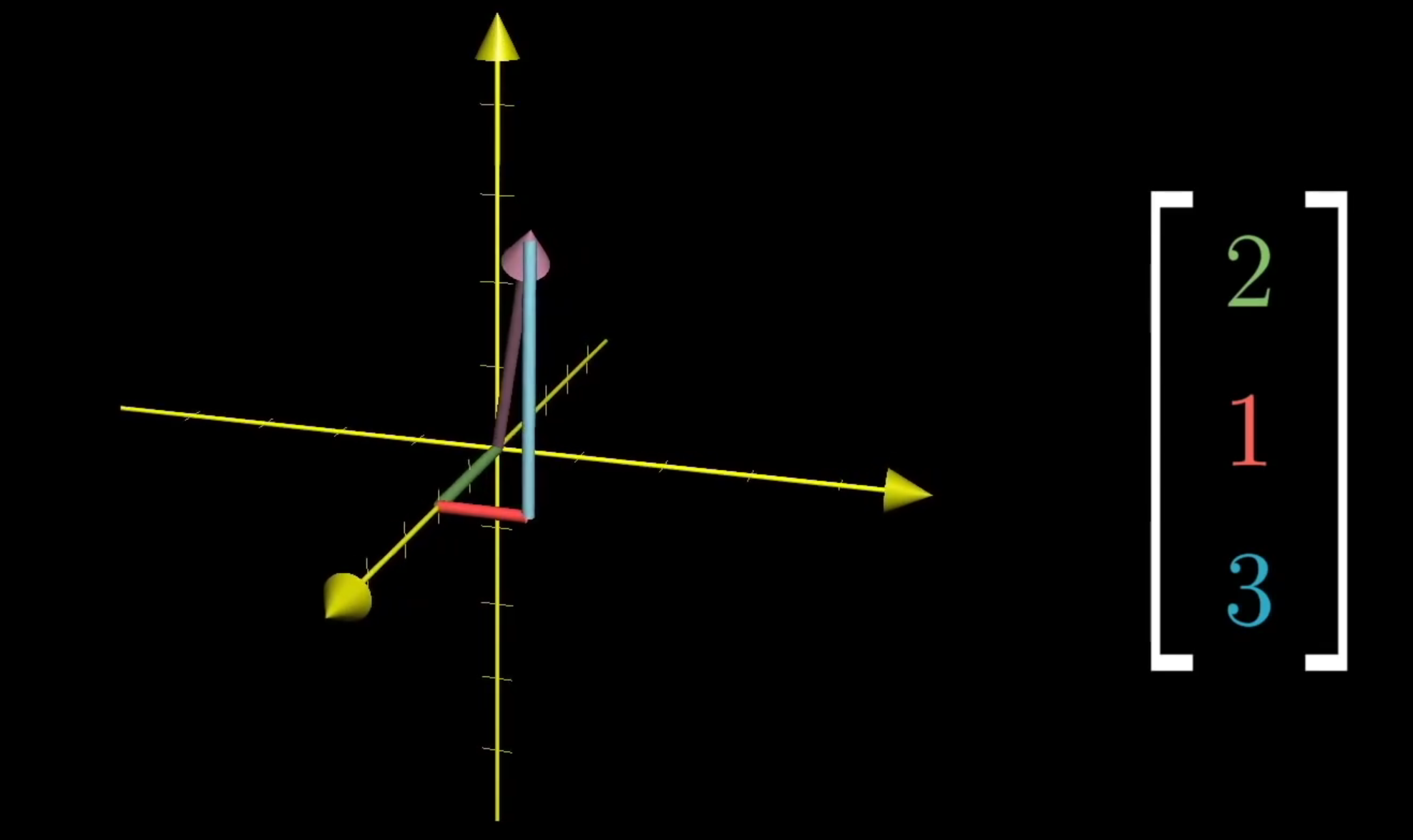
例如,这个列向量代表,是沿x轴走了2个单位长度,沿y轴走了1个单位长度,沿z轴走了3个单位长度而形成的向量
- 向量可以是任何东西,只需要保证:两个向量相加及数字与向量相乘是有意义的即可
- 向量加法和向量乘法贯穿线性代数始终,十分重要
1.2 坐标系
把向量置于坐标系中,坐标正负表示方向,原点为起点,可完美把两个不同的角度融合
- 向量加法
- 物理:首尾相连 Motion
- 计算机:坐标相加
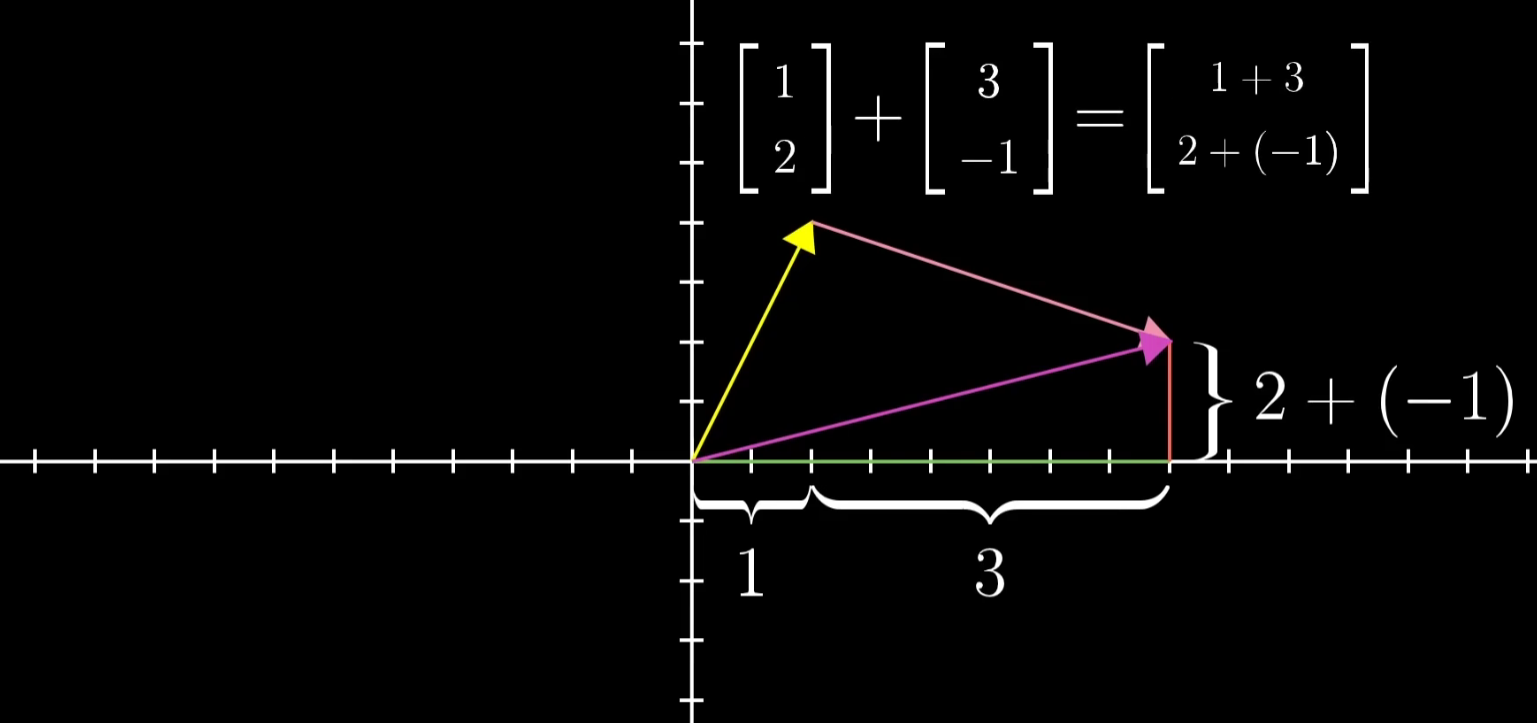
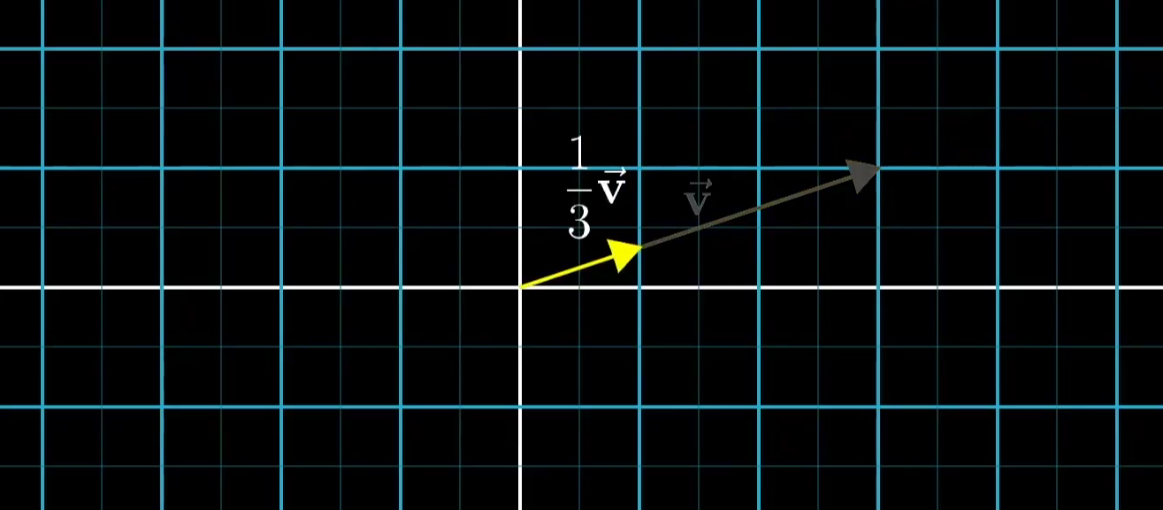
- 向量乘法
- 物理:缩放 Scaling
- 计算机:坐标和比例相乘
数学需要的不是天赋,而是少量的自由想象,但想象太过自由又会陷入疯狂 ——安古斯 · 罗杰斯
Mathematics requires a small dose, not of genius, but of an imaginative freedom which, in a larger dose, would be insanity - Angus K. Rodgers
本部分继续加深一个概念,为何向量加法与向量乘法是那么重要,并从始至终贯穿整个线性代数
1.3 线性组合
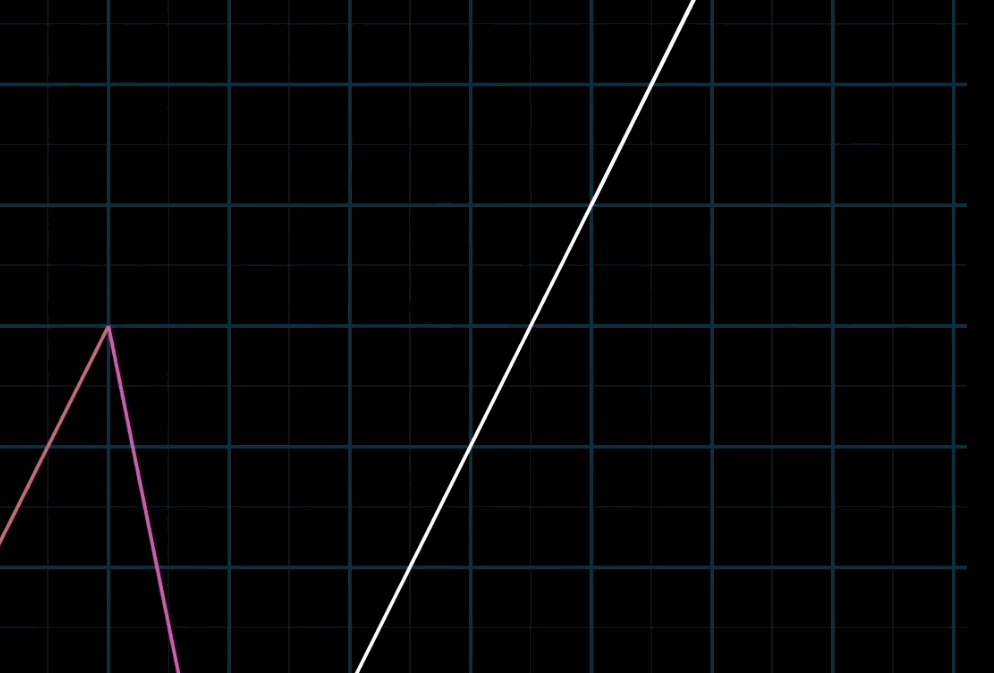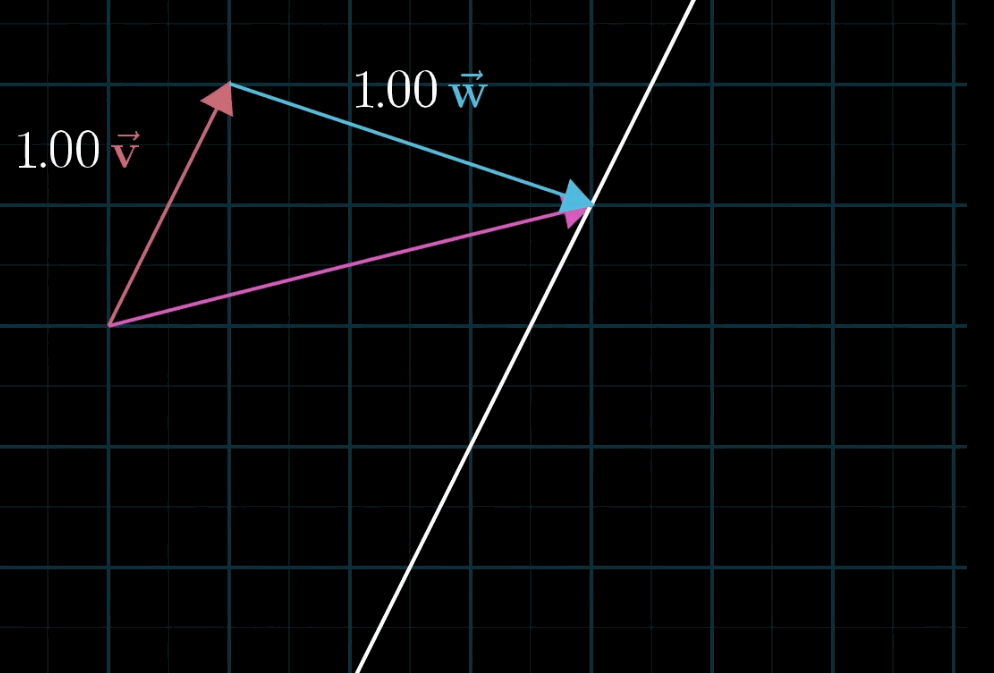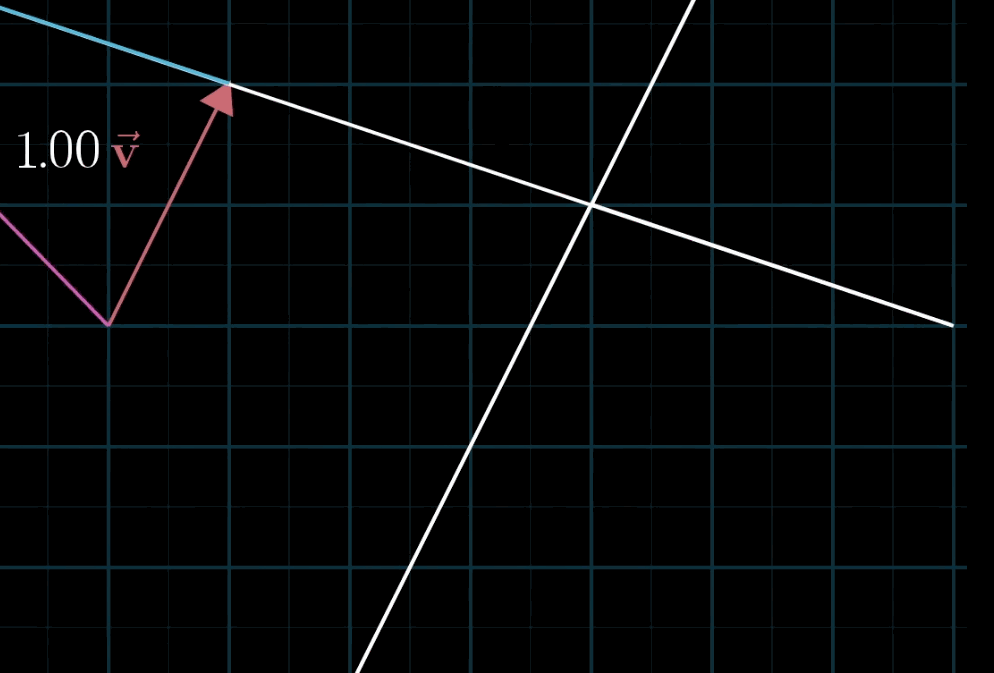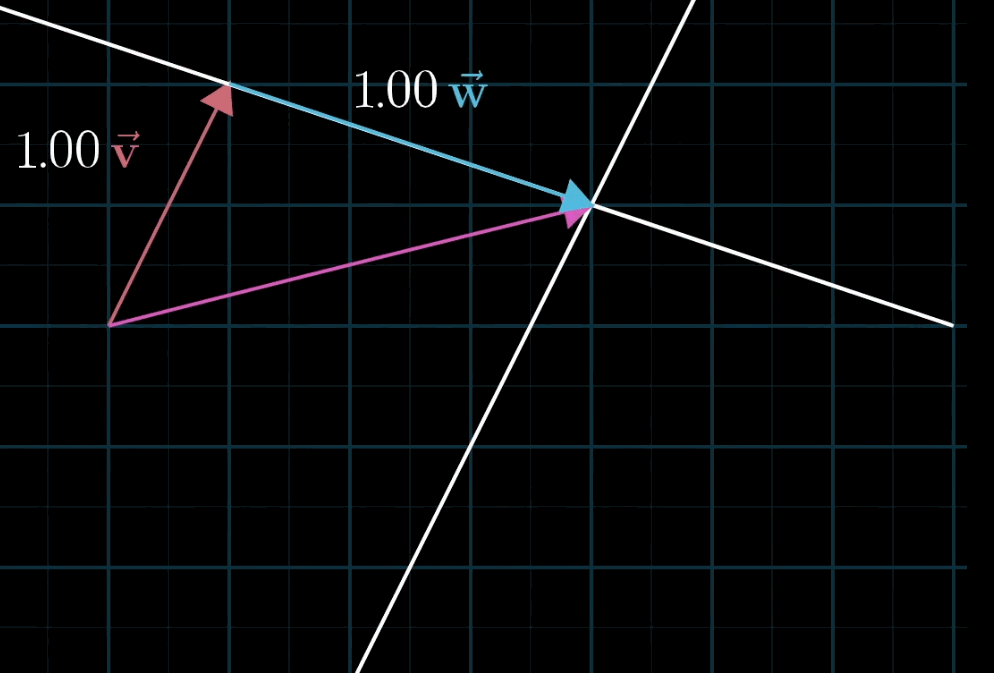
这个概念再好理解不过,空间中不共线的两个不为零向量都可以表示空间中的任意一个向量,写成符号语言就是:$a \mathbf{\vec v} + b \mathbf{\vec w}$
至于为什么被称为 “线性”,有一种几何直观:如果你固定其中一个标量,让另一个标量自由变化,所产生的向量终点会描出一条直线
1.4 空间的基 Basis
对于我们常见的笛卡尔坐标系,有一个最直观一组基:${ {\hat {\imath} } ,{\hat {\jmath} } }$ ,即单位向量:${\hat {\imath} }=(1,0)$ 和 $\hat {\jmath} =(0,1)$ ,通过 ${\hat {\imath} }$ 和 ${\hat {\jmath} }$ 的拉伸与相加可以组成笛卡尔坐标系中的任意一个向量
1.4.1 张成的空间 Span
同理,举一反三的来说,我们可以选择不同的基向量,并且这些基向量构成的空间称为:张成的空间。张成二字比较拗口,可以类比为延展或扩展。直观来看,就是所有动图中的网格。笛卡尔坐标系就是一个由单位坐标 ${ {\hat {\imath} } ,{\hat {\jmath} } }$ 张成的空间
所有可以表示为给定向量(基)线性组合(刚刚讲了这个概念)的向量的集合,被称为给定向量(基)张成的空间
如果你继续思考一下,会发现一个特点:并不是每一组给定向量都可以张成一个空间,若这两个向量共线(2D),共面(3D),它们就只能被限制在一个直线或面中,类似于 “降维打击”。通过这个直观的思考可以引出一个概念:线性相关
1.4.2 线性相关
关于什么是线性相关,有两种表达
- 【表达一】你有多个向量,并且可以移除其中一个而不减小张成的空间(即 2D 共线或 3D 共面),我们称它们(这些向量)线性相关
- 【表达二】其中一个向量,可以表示为其他向量的线性组合,因为这个向量已经落在其他向量张成的空间之中
如果从统计学角度来说,这些向量之中有冗余。这一堆向量中,我们只需要其中几个(取决于维度)就可以表示其他所有的向量。
1.4.3 向量空间一组基的严格定义
有了这些对名词(概念)的直观理解,来看看数学家们是如何严谨的定义向量空间的一组基:
向量空间的一组基是张成该空间的一个线性无关向量集
2. 矩阵与线性变换
很遗憾,Matrix(矩阵)是什么是说不清的。你必须得自己亲眼看看 ——墨菲斯
Unfortunately, no one can be told what the Matrix is. You have to see it yourself -Morpheus
矩阵,最直观的理解当然是一个写成方阵的数字 $\left[\begin{smallmatrix} 1&2 \ 3&4 \end{smallmatrix}\right]$,这几节的核心是为了说明:矩阵其实就是一种向量变换(至于什么是变换下面会讲),并附带一种不用死记硬背的考虑矩阵向量乘法的方法
2.1 变换
变换本质上是函数的一种花哨的说法,它接受输入内容,并输出对应结果。

但【变换】的表达方法暗示了我们可以用运动的方法来理解【向量的函数】这一概念,可以用可视化的方法来展现这组【变换】即输入 - 输出关系
这世界上有非常多优美的变换,如果你将他们编程,并可视化,就能得到下图

2.2 线性变换
我们说具有以下两个性质的就是线性变换(直观可视化如下图):
- 直线在变换后仍然保持为直线,不能有所弯曲
- 原点必须保持固定
一句话总结来说是:线性变换是 “保持网格线平行且等距分布” 的变换
2.3 如何用数值描述线性变换
这里需要使用上一节提到的工具,空间的基,也就是单位向量(基向量):${\hat {\imath} }=(1,0)$ 和 $\hat {\jmath} =(0,1)$
你只需要关注两个基向量 $\hat {\imath}$ 和 $\hat {\jmath}$ 变换后的位置即可。例如, $\hat {\imath}$ 变换到 $(3,1)$ 的位置, $\hat {\jmath}$ 变换到 $(1,2)$ 的位置,并把 $\hat {\imath}$ 变换后坐标立起来作为方阵的第一列(绿色表示), $\hat {\jmath}$ 变换后的坐标立起来作为方阵的第二列(红色表示)。
构成了一个矩阵:$\begin{bmatrix} \color{green}3&\color{red}1 \ \color{green}1&\color{red}2 \end{bmatrix}$,假设我们想要知道目标向量 $(-1,2)$ 进行变换后的位置,那么这个矩阵就是对变换过程最好的描述,一动图胜千言
Step1:绿色 $\hat {\imath}$ (x 轴)进行移动(变换)
Step2:红色 $\hat {\jmath}$ (y 轴)进行移动(变换)
Step3:目标向量 x 轴坐标值与 $\hat {\imath}$ 变换后向量进行向量乘法
Step4:目标向量 y 轴坐标值与 $\hat {\jmath}$ 变换后向量进行向量乘法
Step5:两者进行向量加法,得到线性变换结果
更加一般的情况,我们用变量来代替其中的具体值:绿色代表 $\hat {\imath}$ 变换后的向量,红色代表 $\hat {\jmath}$ 变换后的向量
这就是乘法公式的由来。
2.4【线性】的严格定义
在给出一个数学化抽象的解释前,先做一下总结:
- 【线性变换】是操纵空间的一种手段,它保持网格线平行且等距分布,并保持原点不动
- 【矩阵】是描述这种变换的一组数字,或者说一种描述线性变换的语言
在数学上,【线性】的严格定义如下述公式,这些性质,会在之后进行讨论,也可以在这里就进行一些思考,为什么说向量加法和向量乘法贯穿线性代数始终,毕竟是线性代数,很重要的名次就是线性二字
3.矩阵乘法与变换复合的联系
据我的经验,如果丢掉矩阵的话,那些涉及矩阵的证明可以缩短一半 ——埃米尔 · 阿廷
It is my experience that proofs involving matrices can be shortened by 50% if one throws the matrices out -Emil Artin
3.1 复合变换
如果对一个向量先进行一次旋转变换,再进行一次剪切变换 保持不变第一列为(1,0), 移动到坐标(1,1) ,如下图所示
那么如果通过旋转矩阵和剪切矩阵来求得这个符合矩阵呢?为了解决这个问题,我们定义这个过程叫做矩阵的乘法
3.2 矩阵乘法
在这里我们发现,矩阵乘法的变换顺序是从右往左读的(这一个常识很重要,你得明白这一点,有基本概念),进一步联系和思考发现,和复合函数的形式,如 $f(g(x))$ ,是一致的
那么如何求解矩阵乘法呢?对线性代数有印象的同学你们现在能马上记起来那个稍显复杂的公式吗?如果有些忘记了,那么,现在,就有一个一辈子也忘不了的直观解释方法:
M1矩阵的第一列表示的是 $\hat {\imath}$ 变换的位置,先把它拿出来,M2矩阵看成对这个变换过的 $\hat {\imath}$ 进行一次变换(按照同样的规则),就如上图所示。同理,针对 $\hat {\jmath}$ 一样的操作过程,就可以得出这个表达式。这里我也不把它写出来了,按照这种思路,并且把上面的动图多看几遍,如果还能忘记,那就要去补一补基本的对几何图形的反应能力了(这也是一种能力,包括三维想象力,心算能力,都和记忆或肌肉一样,不锻炼,是不可能躺着被提高的)
3.3 计算规则证明
有了上面的想法,可以自己尝试证明一下,矩阵乘法的交换律是否成立?矩阵乘法的结合律呢?你会发现,原来这么直观,根本不需要动笔算
3.4 三维空间
对三维空间内扩展的话,你会发现,显示生活中的每一种形态改变都能用一个3*3的矩阵来表示这个变换,这在机器人,自动化操作领域是非常重要的,因为你可以把现实生活很难描述的动作通过一个矩阵来表示,是一个连接数字和现实的重要桥梁和工具
4.行列式
计算的目的不在于数字本身,而在于洞察其背后的意义 ——理查德 · 汉明(没错,是发明汉明码的那个人)
The purpose of computation is insight, not numbers - Richard Hamming
4.1 行列式定义的由来
我们注意到,有一些变换在结果上拉伸了整个网格,有一些则是压缩了,那如何度量这种压缩和拉伸呢?或者换一种更容易思考的表达,某一块面积的缩放比例是多少?
其实,根据我们之前讲的基向量,我们只需要知道 $\hat {\imath}$ 和 $\hat {\jmath}$ 组成的面积为 1 的正方形面积缩放了多少就代表所有的情况。因为线性变换有一个性质:网格线保持平行且等距分布
所以,这个特殊的缩放比例,即线性变换对面积产生改变的比例,就是行列式
特别的,我们可以发现,如果一个矩阵的行列式为 0,意味着它把这个空间降维了,并且矩阵的列线性相关
其中,正负表达的是方向,类似于纸的翻面。从数学来说,$\hat {\jmath}$ 起始状态在 $\hat {\imath}$ 的左侧,如果经过变换,变为在右侧,就添加负号。三维情况下,右手定位为正
4.2 计算行列式
为了连接行列式的计算公式和几何直观,我们现考虑 $\begin{bmatrix} \color{green}a&\color{red}b \ \color{green}c&\color{red}d \end{bmatrix}$ 其中的b c 为 0,那么,a 表示 $\hat {\imath}$ 在x轴缩放比例,d 表示 $\hat {\jmath}$ 在y轴缩放比例,ad表示拉伸倍数,同理来说,bc表示的就是压缩倍数,两者的和就是缩放比例。如果你还是对公式念念不忘,那么下面这张图可能可以帮到你
4.3 行列式直观理解的好处
在这里,可以思考一下如何证明 $det(M_1M_2) = det(M_1)det(M_2)$ ,你会发现太简单不过了
5.逆矩阵、列空间、秩与零空间
提出正确的问题比回答它更难 ——格奥尔格 · 康托尔
To ask the right question is harder than to answer it - Georg Cantor
首先,这一节并不涉及计算的方法,相关名次有:高斯消元法 Gaussian elimination、行阶梯形 Row echelon form。这里着眼的是对抽象的概念建立一个几何直观的理解,计算的任务就交给计算机去做
5.1 矩阵的用途
- 描述对空间的操作,
3*3矩阵描述的三维变换 - 可以帮助我们解线性方程组(Linear System of equation)
5.2 线性方程组
上图就是一个整理好的线性方程组,一般形式 $\mathbf A \mathbf{\vec x} = \mathbf{\vec v}$ ,其中 $\mathbf{\vec x}$ 是待求向量。使用之前的几何直观来翻译个公式即,$\mathbf{\vec x}$ 经过 $\mathbf A$ 矩阵变换后,恰好落在 $\mathbf{\vec v}$ 上,如下图
既然使用了 $\mathbf A$ 这个矩阵变换,那么之前讲解的概念:行列式应用在这里就很有意思了。根据之前提到的,行列式直观来说就是矩阵变换操作面积的缩放比例。我们可以思考,$det(\mathbf A) = 0$ 意味着缩放比例为 0,即降维了。很大可能找不到解,唯一的可能性,比如平面压缩成直线,这个直线恰好落在 $\mathbf{\vec v}$ 上才有解。这也是为什么计算行列式的值可以判断方程是否有解的几何直观
接下来思考如何求 $\mathbf{\vec x}$ 。逆向思考,从 $\mathbf{\vec v}$ 出发,进行某一个矩阵变换,恰好得到 $\mathbf{\vec x}$ 。而这个反过来的矩阵变换,就称为 $\mathbf A$ 矩阵的逆矩阵,写成公式是:
5.3 逆矩阵
所谓逆,就是反过来的意思。根据基向量代表整个空间,已经变换过的 $\hat {\imath}’$ 和 $\hat {\jmath}’$ 如何通过一个矩阵变换,变回 $\hat {\imath}$ 和 $\hat {\jmath}$ ,这个矩阵就是逆矩阵 ,写作 $\mathbf A^{-1}$,直观理解如下图
逆矩阵乘原矩阵等于恒等变换,写作 $\mathbf A \mathbf A^{-1} = \mathbf I$ 。$\mathbf I$ 矩阵表示基向量,对角线元素为 1,其余为 0(矩阵说对角线,默认为左上方到右下方)
5.4 列空间
其实这只是之前一直在提到过的概念,在线性方程组中,这么描述:所有可能得输出向量 $\mathbf A \mathbf{\vec v}$ 构成的集合被称为 A 的列空间。这么说不太好理解,可以从名称 “列空间” 入手,矩阵的列是什么呢?我们之前已经多次强调了,就是 $\hat {\imath}$ 和 $\hat {\jmath}$ 变换后的坐标。即矩阵的列表示基向量变换后的坐标(位置),变换后的向量张成的空间就是所有可能得输出向量
简单说即:列张成的空间 = 列空间,即矩阵的列所张成的空间,如下图。
检查一下自己是否完全理解,就思考下面句话为什么这么说:零向量一定在列空间中(列空间很好理解)
5.5 秩 Rank
秩这个概念相信很多学习线性代数的同学,因为中文字,秩,本身就不熟(和正则化有点类似),所以秩也就非常难以理解了。秩是秩序,联想为秩序的程度。但是,因为你已经看了这个教程,矩阵的秩在现在你拥有的几何直观下,理解起来,当真的小菜一碟
我们已经建立了一种深刻的认知:矩阵 = 变换,那么变换后空间的维度,就是这个矩阵的秩。更加精确的定义是:列空间的维数(如果你可以焕然大:原来这两句话是一个意思,那么我觉得你对矩阵的理解已经有了质的提高)
5.6 零空间
变换后落在原点的向量的集合,称为这个矩阵(再次强调矩阵 = 变换的数字表达)的零空间或核,如果感觉没理解,可以看看下图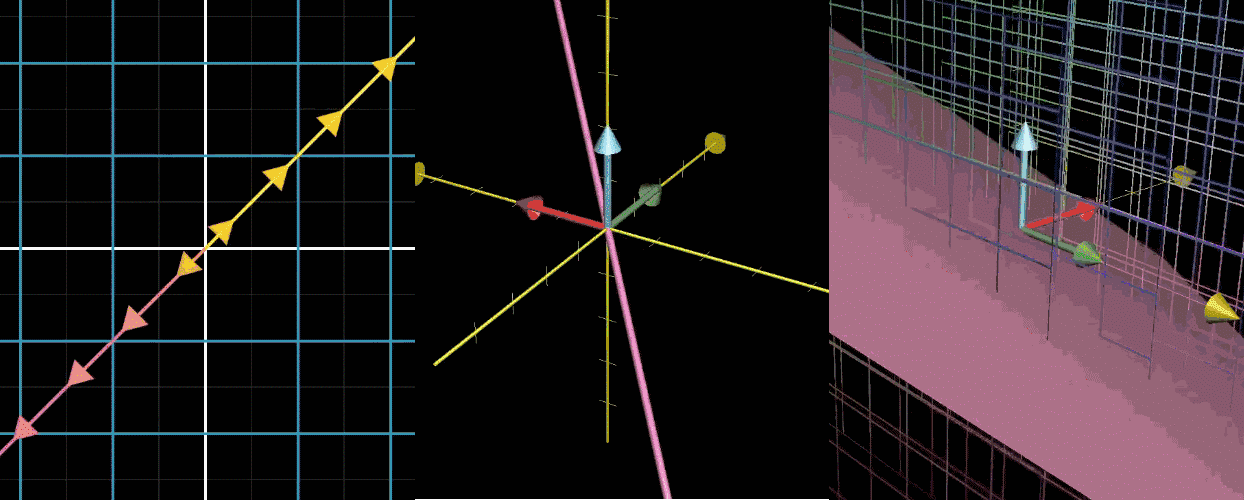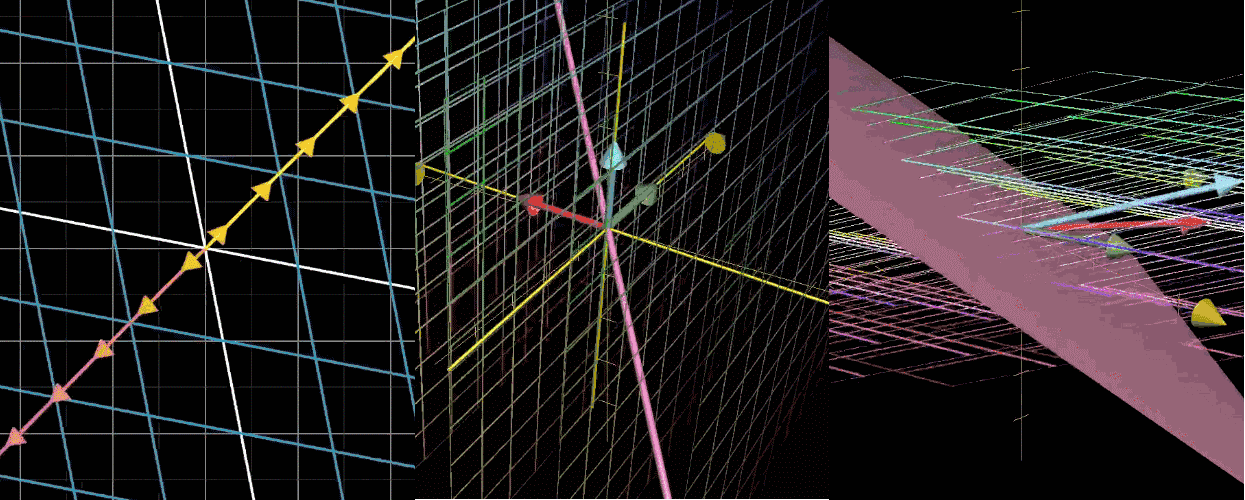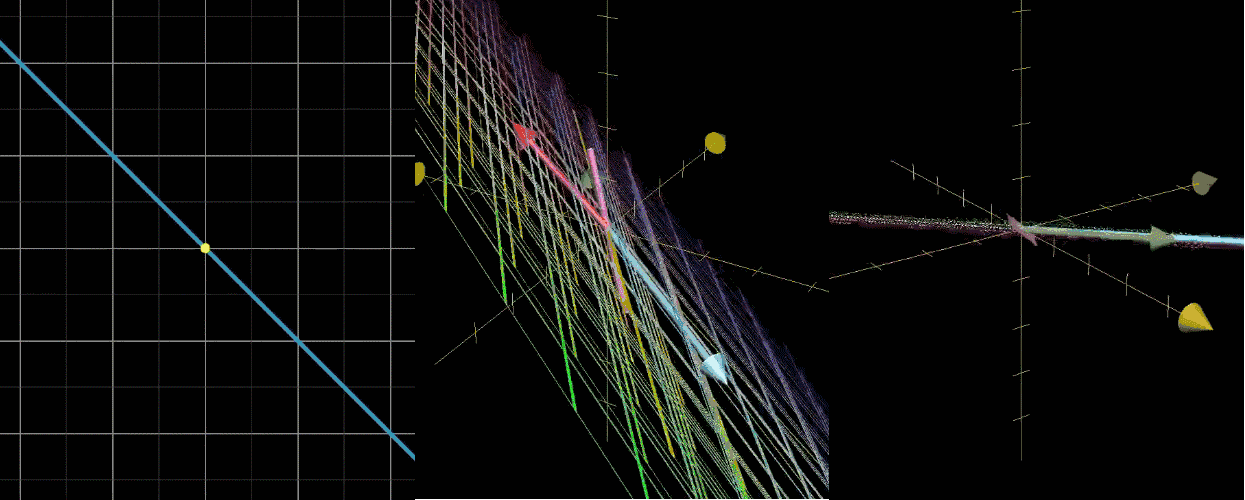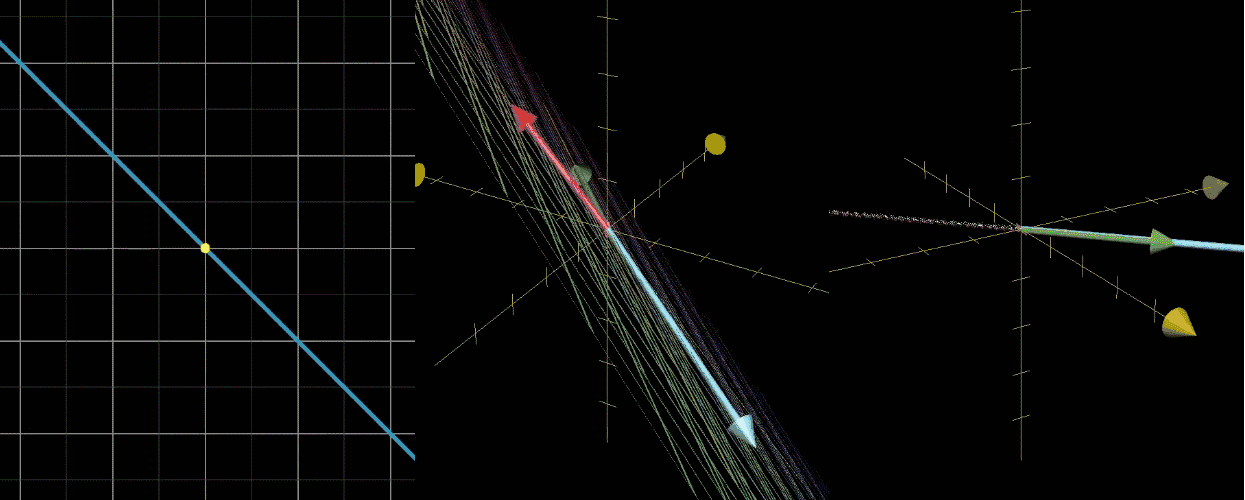
【图 1】二维压缩到一个直线(一维),有一条直线(一维)的点被压缩到原点
【图 2】三维压缩到一个面(二维),有一条直线(一维)的点被压缩到原点
【图 3】三维压缩到一条线(一维),有一条直线(二维)的点被压缩到原点【注意】压缩就是变换,变换就是矩阵,其实说的就是矩阵
满秩 = 列空间 + 零空间
5.7 总结
- 从几何角度理解线性方程组的一个高水平概述
- 每个方程组都有一个线性变换与之联系,当逆变换存在时,你就能用这个逆变换求解方程组
- 不存在逆变换时,列空间的概念让我们清楚什么时候存在解
- 零空间的概念有助于我们理解所有可能得解的集合是什么样的
在这个小测试里,我让你们求一个 2*3 矩阵的行列式。让我感到非常可笑的是,你们当中竟然有人尝试去做 ——佚名
On this quiz, I asked you to find the determinant of a 2*3 matrix. Some of you, to my great amusement, actually tried to do this - no name listed
5.8 几何意义
首先从一个特例出发,考虑3×2(3 行 2 列)矩阵的几何意义,从列空间我们得知,第一列表示的是 $\hat {\imath}$ 变换后的位置(现在是一个有三个坐标的值,即三维),第二列同理是 $\hat {\jmath}$ 。总结来说,3×2矩阵的几何意义是将二维空间映射到三维空间上
此时从特例到一般化推倒,我们可以得到一个结论:n*m 的几何意义是将 m 维空间(输入空间)映射到 n 维空间(输出空间)上
注意这里的输入空间,输出空间的概念,阅读方向同样也是从右向左的(靠右的是输入,靠左的是输出)
5.9 非方阵乘法
如果你已经学过线性代数的大学课程,你可能有一些影响,并不是任意两个非方阵都可以进行矩阵乘法,必须满足一些条件,例如,$\mathbf M_1 \mathbf M_2$(非方阵)计算中,假设 $\mathbf M_2$ 为2×3的矩阵,那么 $\mathbf M_1$ 的列必须等于 $\mathbf M_2$ 的行,否则这个乘法是没法计算的。
当我们有了变换的几何直观后,这个概念只要自己思考推导一次,也是一辈子都忘不了的
直观解释是:矩阵的行是这个变换的输出空间维数,而列是变换的输入空间维数。矩阵乘法从右向左读,第一个变换的 $\mathbf M_2$ 的输出向量的维度( $\mathbf M_2$ 的行)必须和第二个变换 $\mathbf M_1$ 的输入向量( $\mathbf M_1$ 的列)维度相等,才可以计算。也就是说,类似于插头和插座的关系,我只有三头插座,你来一个双头插头肯定没法用的
5.10. 非方阵行列式
这里有一个很好玩的概念,非方阵的行列式呢?都不是一个维度的变换,如同归零者和咱们谈判一样,你和我谈缩放比例?不存在的
6.点积与对偶性
卡尔文:你知道吗,我觉数学不是一门科学,而是一种宗教
霍布斯:一种宗教?
卡尔文:是啊。这些公式就像奇迹一般。你取出两个数,把它们相加时,它们神奇地成为了一个全新的数!没人能说清这到底是怎么发生的。你要么完全相信,要么完全不信
6.1 什么是点积
两个相同维数的向量,或是两个相同长度的数组。求它们的点积,就是将相应坐标配对,求出每一对坐标的乘积,然后将结果相加,一动图胜千言
几何直观来说,$\mathbf{\vec v} \cdot \mathbf{\vec w}$ 可以想象成向量 $\mathbf{\vec w}$ 朝着过原点和向量 $\mathbf{\vec v}$ 的直线上的正交(垂直)投影,然后把投影的长度和向量 $\mathbf{\vec v}$ 的长度乘起来就是点击的值。其中正负号代表方向,两个向量成锐角,大于 0;钝角,小于 0
6.2 点积的顺序
你可能会发现,顺序在线性代数其实是很重要的,而对于 $\mathbf{\vec v} \cdot \mathbf{\vec w}$ 和 $\mathbf{\vec w} \cdot \mathbf{\vec v}$ 它们的结果是相同,为什么呢?
解释的方法为:首先假设 $\mathbf{\vec v}$ 和 $\mathbf{\vec w}$ 长度相同,利用对称轴,两个向量互相的投影相等;接下来如果你缩放其中一个到原来的两倍,对称性被破坏,但是缩放比例没变,最终乘法的结果也没变,一动图胜千言
6.3 点积与投影
这个时候问题就来了,这种直观的乘法与加法的组合运算:点积为何和投影长度的乘积有关?这个问题非常有意思,因为回答这个问题的过程用到了十分精彩的直觉和思维方式
首先,需要建立多维空间到一维空间的线性变换(描述为1×n的矩阵,列代表对应的基向量压缩到一维空间的位置),即函数(自变量对应多维空间,$f(x)$ 最后的输出为一维空间,也就是数轴上的点,一个确定的数)的概念。一动图胜千言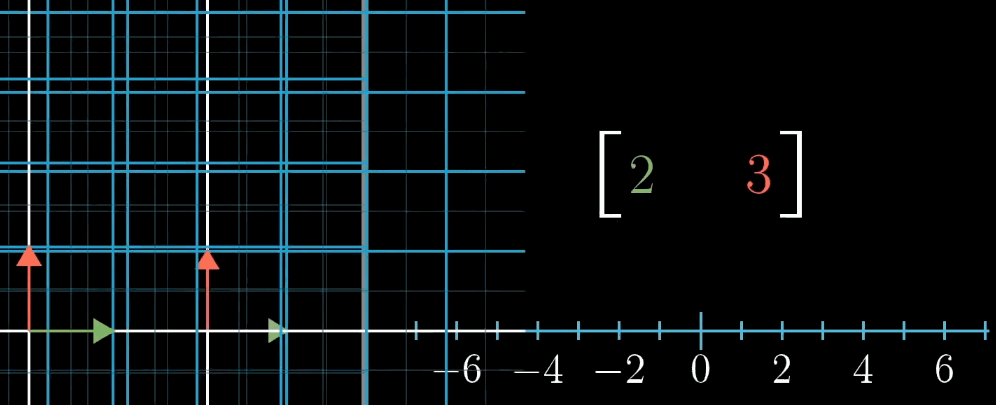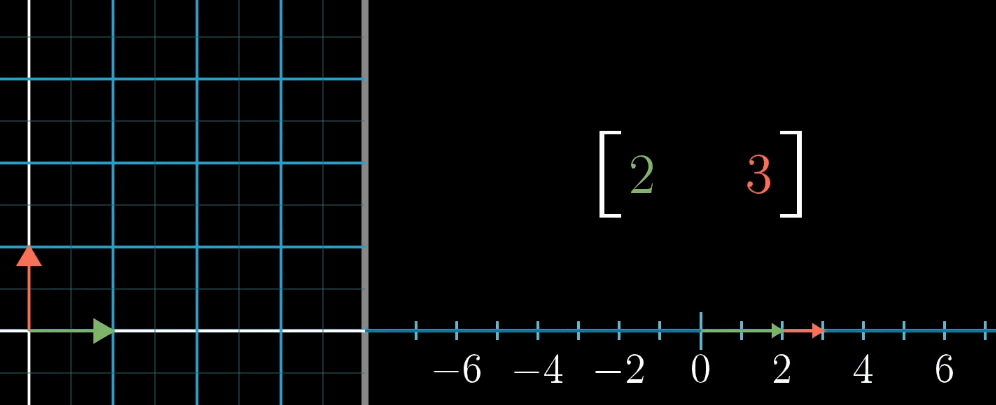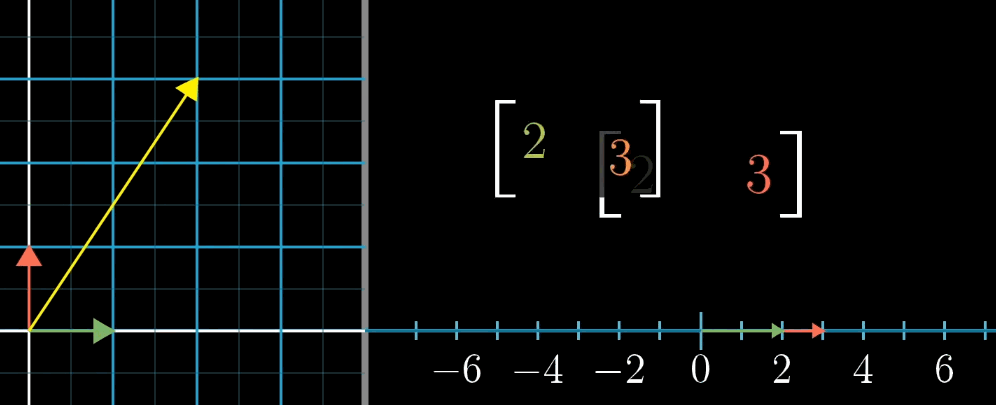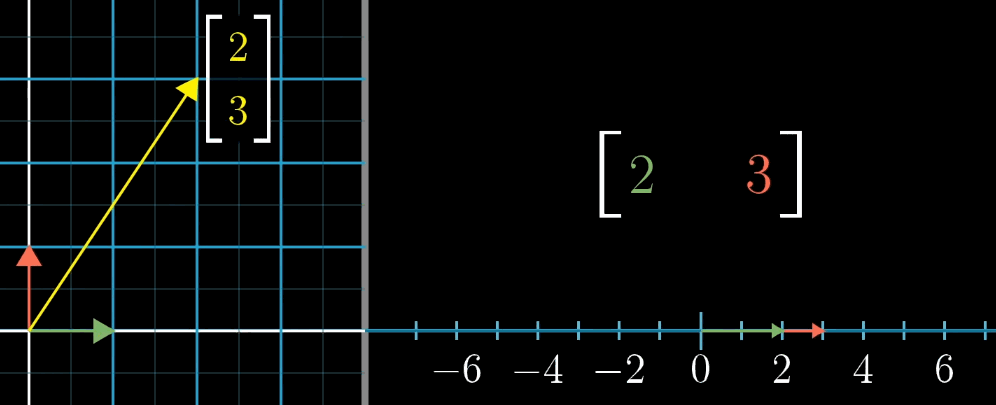
你会发现,n×1 表示的是坐标和1×n表示的多维到一维的变换(矩阵)之间有某种联系,即将向量转化为数的线性变换和这个向量本身有着某种关系
接下来,我们想象一个情景,这个被压缩成的一条线(数轴)放置在一个坐标系(二维空间)中,且空间所有向量都经过一个变换被压缩到这个数轴上。记这个数轴的单位向量为 $\mathbf{\vec u}$,一动图胜千言
再然后,我们需要考虑的问题变为,坐标系中的 $\hat {\imath}$ 与 $\hat {\jmath}$ 是如何被压缩到这条直线上的呢(基向量表征整个空间的变换)?即求一个1×2的矩阵内的值,第一列表示 $\hat {\imath}$ 变换后的位置(在这条数轴上),第二列表示 $\hat {\jmath}$ 变换后的位置。可以直接给出结论,这个变换的数值恰好就是 $\mathbf{\vec u}$ 在这个坐标系中的坐标 $(u_x,u_y)$ ,推倒方法使用到了对称性,一动图胜千言
动图中的白色虚线就是对称轴,目的就是确定变换后 $\hat {\imath}$ 与 $\hat {\jmath}$ 的位置,即描述变换的矩阵(再次重复,列表示坐标,行表示变换)。
推导完毕,把这个过程总结成一个动图
矩阵的向量乘积和点积的计算公式一样,且恰好由压缩这一变换理念,与投影正好联系了起来。关键点,在于压缩变换 = 投影
6.4 对偶性
在证明的过程中,有一个很关键的点就是使用了对称轴(对称理念)。在数学中,对偶性定义为:两种数学事物之间自然而又出乎意料的对应关系。刚刚推倒的内容是数学上 “对偶性” 的一个实例,即无论何时你看到一个二维到一维的变换,空间中会存在为一个向量 $\mathbf{\vec v}$ 与之相关
6.5 总结
- 点积是理解投影的有力几何工具
- 方便检验两个向量的指向是否相同
- 更进一步,两个向量点乘,就是将其中一个向量转化为线性变换
- 向量放佛是一个特定变换的概念性记号。对一般人类来说,想象空间中的向量比想象这个空间移动到数轴上更加容易
7. 叉积
每一个维度都很特别 ——杰弗里 · 拉加里亚斯
从他(格罗滕迪克)和他的作为中,我还学到了一点:不以高难度的证明为傲,因为难度高意味着我们还不理解。理想的情况是能够绘出一幅美景,而其中的证明显而易见
7.1 二维情况下的叉积类比
$\mathbf{\vec v}$ 与 $\mathbf{\vec w}$ 张成的平行四边形的面积,即 $\mathbf{\vec v} \times \mathbf{\vec w}$ ,结果方向的确定考虑 $\hat {\imath}$ 和 $\hat {\jmath}$ 的相对位置关系,与其相同,为正;否则,为负
通过这个定义,结合几何直观,我们可以发现几个有趣的结论
- 越接近垂直的 $\mathbf{\vec v}$ 与 $\mathbf{\vec w}$ 构成的面积越大
- 并且叉积的分配律成立
7.2 真正的叉积定义
真正的叉积是在三维情况下被定义出来的:通过两个三维向量($\mathbf{\vec v}$ 与 $\mathbf{\vec w}$ )产生一个新的三维向量 $\mathbf{\vec p}$ ,向量 $\mathbf{\vec p}$ 的长度就是 $\mathbf{\vec v}$ 和 $\mathbf{\vec w}$ 组成平行四边形的面积 ,向量的方向与平行四边形(所在平面)垂直,并用右手定则确定方向,食指为 $\mathbf{\vec v}$ ,中指为 $\mathbf{\vec w}$ ,大拇指即 $\mathbf{\vec p}$
7.3 叉积计算公式
其中 $\hat {\imath}$ $\hat {\jmath}$ $\hat k$ 三个基向量后的数字就是对应向量 $\mathbf{\vec p}$ 的坐标值
第一次学这个计算方法的时候,估计没几个人能想清楚它为什么是这样的形式,甚至老师也说不清,只是告诉学生,我们这么记下来,定义是这样的定义的。但是,既然是直观讲解,必须把这里的来由探明清楚
7.4 叉积计算的几何直观
在开始前,先再次加深一次对偶性的概念:每当你看到一个(多维)空间到数轴的线性变换时,它都与那个空间中的唯一一个向量对应。即应用线性变换到某个向量和与这个向量点乘等价
恰好,叉积的运算过程给出了对偶性的一个绝佳的实例:根据 $\mathbf{\vec v}$ 和 $\mathbf{\vec w}$ 定义一个从三维空间到数轴的特定线性变换,找到这个变换的对偶向量,这个对偶向量就是 $\mathbf{\vec v}$ 和 $\mathbf{\vec w}$ 的叉积
首先,我们知道三维情况的,求一个3×3矩阵的行列式,就是求这三个向量张成的平行六面体的体积,然后,把第一列(向量)换成一个自变量,后两列(两向量)记为 $\mathbf{\vec v}$ 和 $\mathbf{\vec w}$ ,那么我们就有
这样形式的函数 $f()$ ,如右图所示,即平行六面体随白色向量 $(x,y,z)$ 的随机游走而不断改变。然后,问题就变成了,我们需要根据 $\mathbf{\vec v}$ 和 $\mathbf{\vec w}$ 找到一个变换(一个矩阵,或者说函数),使得上述等式成立。
并且因为 $f()$ 是线性的,可以利用对偶性,一动图胜千言
对偶性:即应用线性变换到某个向量和与这个向量点乘等价,即我们可以把1×3的变换(矩阵用来描述变换),立起来(转置),并写成点乘的形式。并把这个向量记为 $\mathbf{\vec p}$
其中向量的颜色左右对应,并且行列式的值就是右图中平行四面体的体积,然后,我们就把问题进一步变成了:寻找向量 $\mathbf{\vec p}$ 使得上述等式成立
根据点积的性质得知,当你把一个向量与其他向量点积的几何解释是,把其他向量投影到 $\mathbf{\vec p}$ 上,然后将投影长度与 $\mathbf{\vec p}$ 的长度相乘。而我们知道,对于一个平行六面体来说,体积等于底面积乘以高,高于底面积垂直,所以,作为背投影对象的 $\mathbf{\vec p}$ 必须和 $\mathbf{\vec v}$ 和 $\mathbf{\vec w}$ 构成的平面垂直,方面已经找到
至于长度,可以看到,一个向量与其他向量点积的几何解释是,把其他向量投影到 $\mathbf{\vec p}$ 上,然后将投影长度与 $\mathbf{\vec p}$ 的长度相乘,其中投影长度就是 $(x,y,z)$ 向量的长度,根据公式的形式,可以观察得,向量 $\mathbf{\vec p}$ 的长度作为第二项,只有当长度等于平行四面体面积时,上述公式(图片中的点积 = 行列式值的公式)才能成立。
至此,又一次利用对偶性发现了一些事物之间自然而又出乎意料的对应关系。通过几何直观来了解计算公式的由来,也是一种加深印象,深刻理解的有效途径
7.5 总结
在这里总结一下涉及到的过程,也可以通过阅读看看是否直观的理解每句话来判断掌握程度
- 首先定义了一个三维空间到数轴的线性变换(函数 $f()$ ),它是根据向量 $\mathbf{\vec v}$ 和 $\mathbf{\vec w}$ 来定义的
- 接着通过两种不同的方式来考虑这个变换的对偶向量
- 这种计算方法引导你在第一列中插入 $\hat {\imath}$ $\hat {\jmath}$ $\hat k$ ,然后计算行列式
- 在几何直观上,这个对偶向量一定与 $\mathbf{\vec v}$ 和 $\mathbf{\vec w}$ 垂直,并且其长度与这两个向量张成的平行四边形的面积相同
8. 基变换
数学是一门赋予不同事物相同名称的艺术 ——昂利 · 庞加莱
Mathematics is the art of givinh the same name to different things -Henri Poincare
8.1 坐标系与基向量
坐标系指:发生在向量与一组数之间的任意转化,如果假设有一个向量,使用 $\hat {\imath}$ 和 $\hat {\jmath}$ 来描述是 $[\begin{smallmatrix} 3 \ 2 \end{smallmatrix}]$ ,我们把这种描述称为:我们的语言。如果有另一组基向量,$\hat {\imath}’ = [\begin{smallmatrix} 2 \ 1 \end{smallmatrix}] $ 和 $\hat {\jmath}’ = [\begin{smallmatrix} -1 \ 1 \end{smallmatrix}]$ (写成列向量的形式是为了形式上的统一)来描述同样一个向量变成 $[\begin{smallmatrix} \frac{5}{3} \ \frac{1}{3} \end{smallmatrix}]$ ,我们把这种语言记为:詹妮弗的语言
8.2 基变换
我们在之前的解释中已经说明了,在不同的【语言】之间的转化使用矩阵向量乘法,在上面的例子中,转移矩阵是 $\mathbf T = [\begin{smallmatrix} 2 & -1 \ 1 & 1 \end{smallmatrix}]$ ,矩阵的列表示用我们的语言表达詹妮弗的基向量,称为基变换。
反过来,就是求转移矩阵的逆 $\mathbf T^{-1}$ ,称为基变换矩阵的逆,作用是可以表示从詹妮弗的基向量转换回我们的语言需要做的变换。
8.3 如何转化一个矩阵
接下来使用一个具体的例子:变换左旋转 90°,在我们的语言中,和詹妮弗的语言分别是如何互相转换的来加深印象
- 左乘基变换矩阵(矩阵的列代表的是用我们的语言描述詹妮弗语言的基向量):需要被转换的詹妮弗的语言:$[\begin{smallmatrix} -1 \ 2 \end{smallmatrix}]$ ➜ 使用我们的语言描述来描述同一个向量
- 左乘线性变换矩阵(表示的变化为:左旋转 90°):➜变换的后的向量(还是以我们的语言来描述)
- 左乘基变换矩阵的逆:➜变换后的向量(用詹妮弗的语言来描述)
这三个矩阵合起来就是用詹妮弗语言描述的一个线性变换
8.4 总结
表达式 $\mathbf A^{-1} \mathbf M \mathbf A$ 暗示着一种数学上的转移作用
- 中间的 $\mathbf M$ 代表一种你所见的转换(例子中的 90° 旋转变换)
- 两侧的矩阵 $\mathbf A$ 代表着转移作用(不同坐标系间的基向量转换),即就是视角上的转换
- 矩阵乘积仍然表示着同一个变换,只不过从其他人的角度来看
这给了很多域变换的应用一个直观的理解,把这简单的几行记录清晰,
在这一部分中,你会发现,前面提到的所有几何直观:线性变换,行列式,线性方程组,基变换会穿插其中。不仅给了你一个机会检验之前的理解是否深刻(在这一节,会添加一些超链接,方便你进行复习和定位),更多的,现在,是拼装起来感受成就感的时刻了!
9. 特征值与特征向量
9.1 What
首先,我们假设坐标系的一个基变换(对 $\hat {\imath}$ 和 $\hat {\jmath}$ 张成的空间做一个线性变换 ),即 $\hat {\imath}’ = [\begin{smallmatrix} 3\ 0 \end{smallmatrix}] $ 和 $\hat {\jmath}’ = [\begin{smallmatrix} 1 \ 2 \end{smallmatrix}]$ 。在变换的过程中,空间内大部分的向量都离开了它所张成的空间(即这个向量原点到终点构成的直线) ,还有一部分向量留在了它所张成的空间,矩阵对它仅仅是拉伸或者压缩而已,如同一个标量。
如上图,是给出例子中,x 轴所有向量被伸长为原来的 3 倍,一个明显留在张成空间内的例子。另一个比较隐藏的,是 $(-1,1)$ 这个向量,其中的任意一个向量被伸长为原来的 2 倍
- 变换中被留在张成空间内的向量,就是特征向量(上例 x 轴和 $(-1,1)$)
- 其中每个向量被拉伸或抽缩的比例因子,就是特征值(上例 3 和 2)
- 正负表示变换的过程中是否切翻转了方向
9.2 Why
三维情况,如果能找到这个不变的向量,即旋转轴(特征值必须为 1)
理解线性变换的作用的关键(或者说更好的描述一个变换),更好的方法是求出它的特征向量和特征值
9.3 How
从计算角度来看特征值和特征向量,里面包含了很多对以前只是回顾和整合
根据特征向量和特征值的定义,使用数学的方法来表示即
$\mathbf A$ 是求特征值和特征向量的变换矩阵;$\mathbf{\vec v}$ 是特征向量;$\lambda$ 是特征值;目标是找 $\mathbf{\vec v}$ 和 $\lambda$
至于为何会用这个式子来定义特征向量和特征值呢,我们继续观察这个式子中的 $\lambda \mathbf{\vec v}$ ,考虑到右边是一个矩阵乘法,我们希望左右都是一个矩阵乘法,这样方便等价和计算。观察发现,$\lambda \mathbf{\vec v}$ 就是给 $\mathbf{\vec v}$ 中每一个元素都乘以 $\lambda$ 。对角矩阵 $\mathbf I$ 且对角线元素为 $\lambda$ 的矩阵也能有同样的变换结果,得到下列表达式
观察这个等式你会发现:可以把 $\mathbf A - \lambda \mathbf I$ 矩阵看成一个对 $\mathbf{\vec v}$ 矩阵的变换,目的是把 $\mathbf{\vec v}$ 压缩到更低的维度。而空间压缩对应的恰好就是变换矩阵的行列式为 0(期待你在品读这句话的时候感受到满满的成就感,实在有难度,再结合下图)
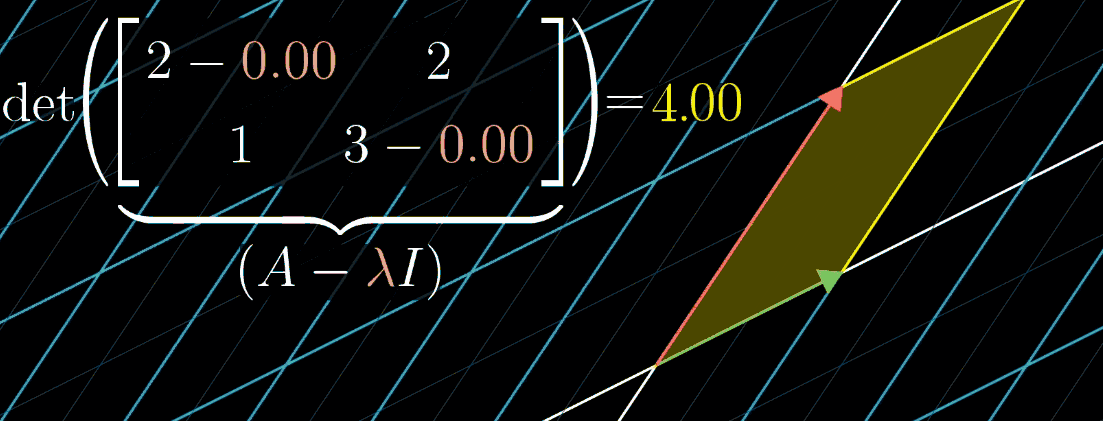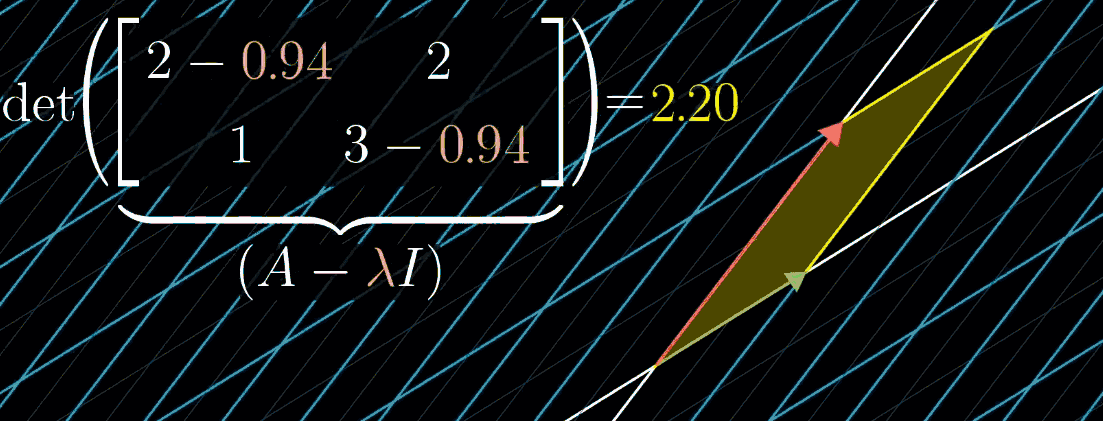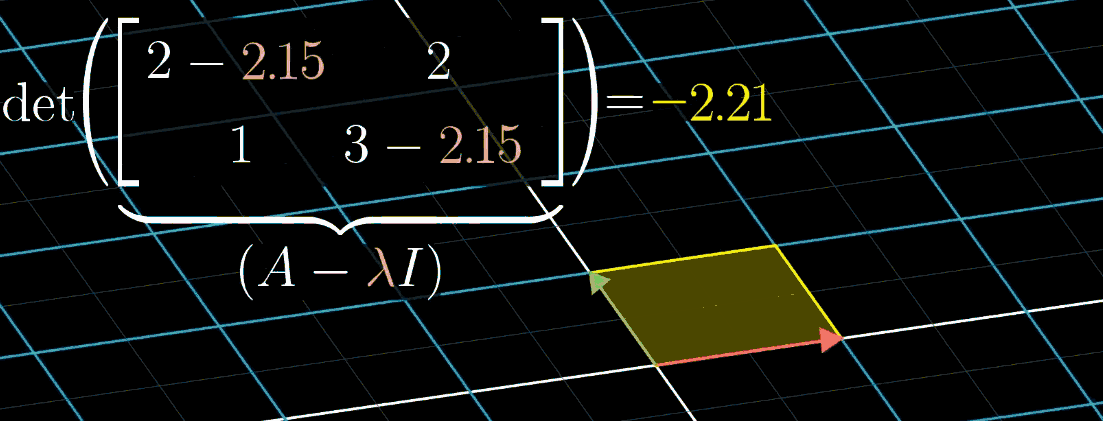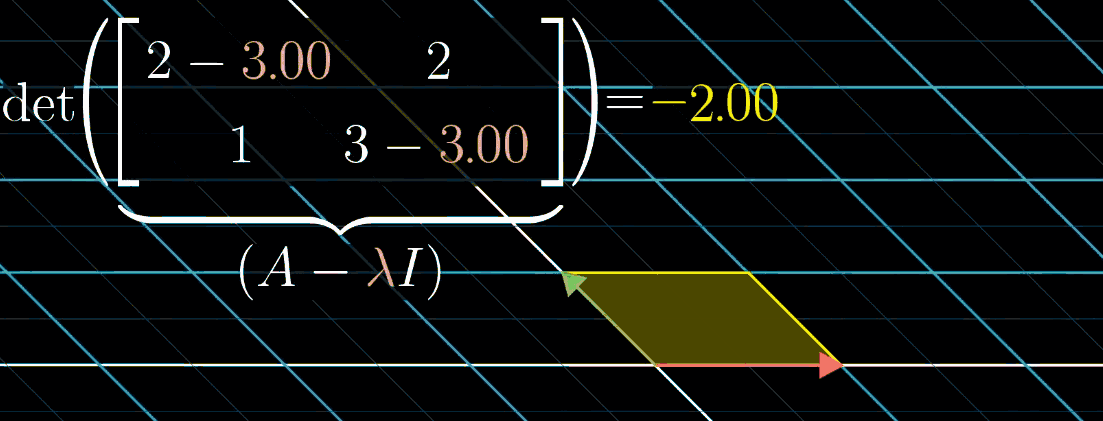
上图显示随 $\lambda$ 可视化的变化情况,从这幅图中,使用的例子是 $[\begin{smallmatrix} 2 & 2 \ 1 & 3 \end{smallmatrix}]$ ,特征值恰好是 1
9.4 特征向量的特殊情况
旋转变换
解出特征值能发现答案是 $\pm i$ ,没有特征向量存在,即特征值出现复数的情况一般对应于变换中的某种旋转
剪切变换
Shear 变换。x 轴不变,只有一个特征值,为 1($(\lambda-1)^2=0$)
伸缩变换
特征值只有一个,但是是空间中所有的向量都是特征向量
9.4 特征基
对角矩阵:只有对角线非零的矩阵。解读它的方法是:所有的基向量都是特征向量。因为之前提到过,矩阵的第一列是 $\hat {\imath}$ ,第二列是 $\hat {\jmath}$ ,往后同理。这样就能发现,如果一列只有对应的位置非零,那么这个坐标轴本身就就是特征向量
一组基向量(同样是特征向量)构成的集合被称为一组:特征基
对角矩阵有一个好处是计算方便,多次矩阵乘法非常容易
这时我们就希望利用对角矩阵(基向量为特征向量)的便于计算的特性,利用上一节提到的基向量变换的方法,把特征向量作为基,对每一个矩阵进行变换后再进行计算,最后再左乘变换矩阵的逆求回原矩阵得到结果,如下图所示
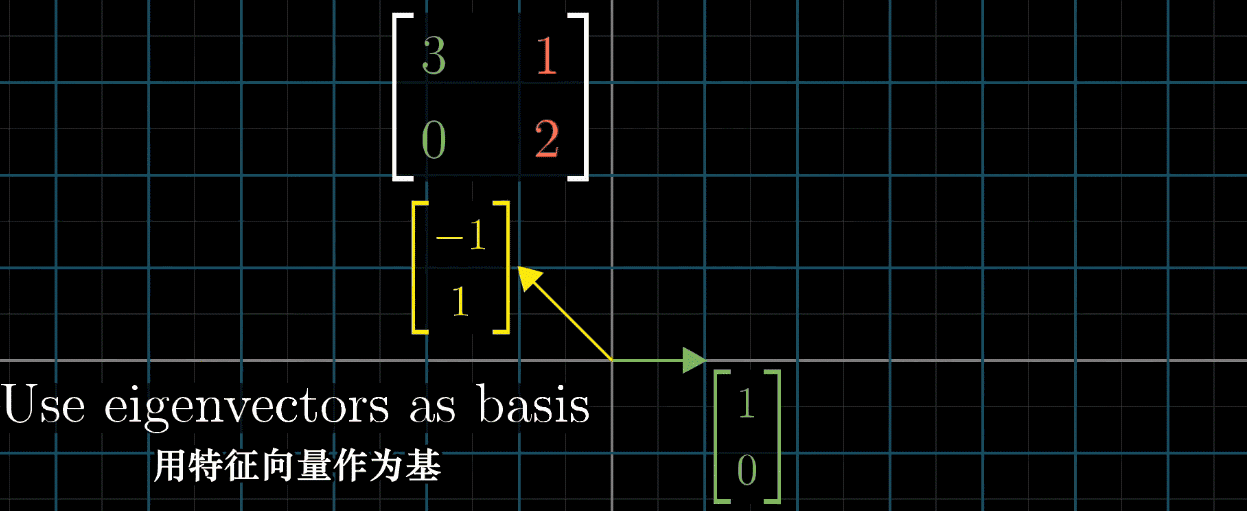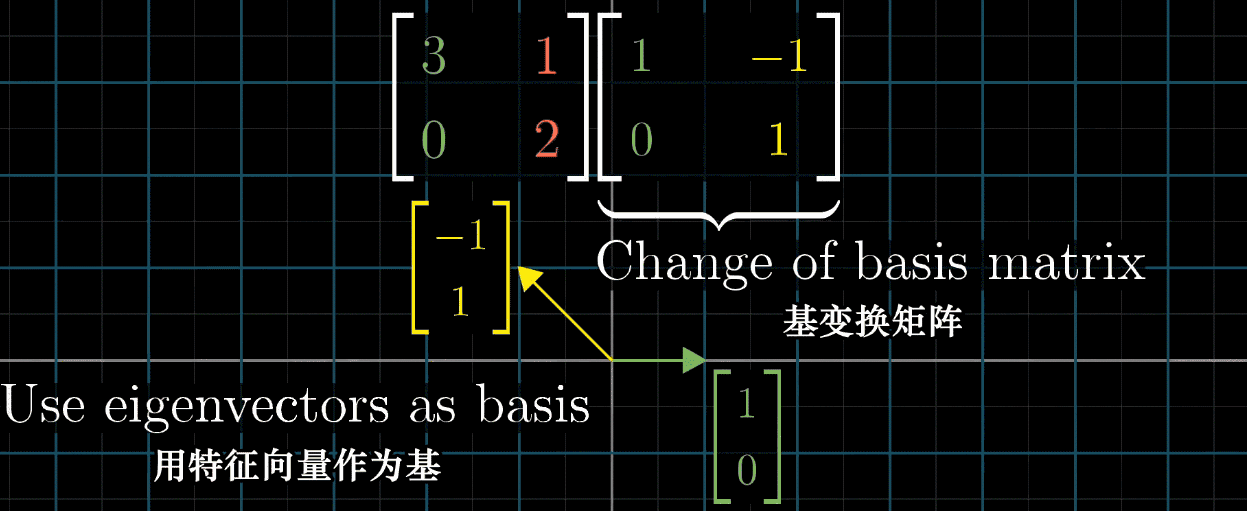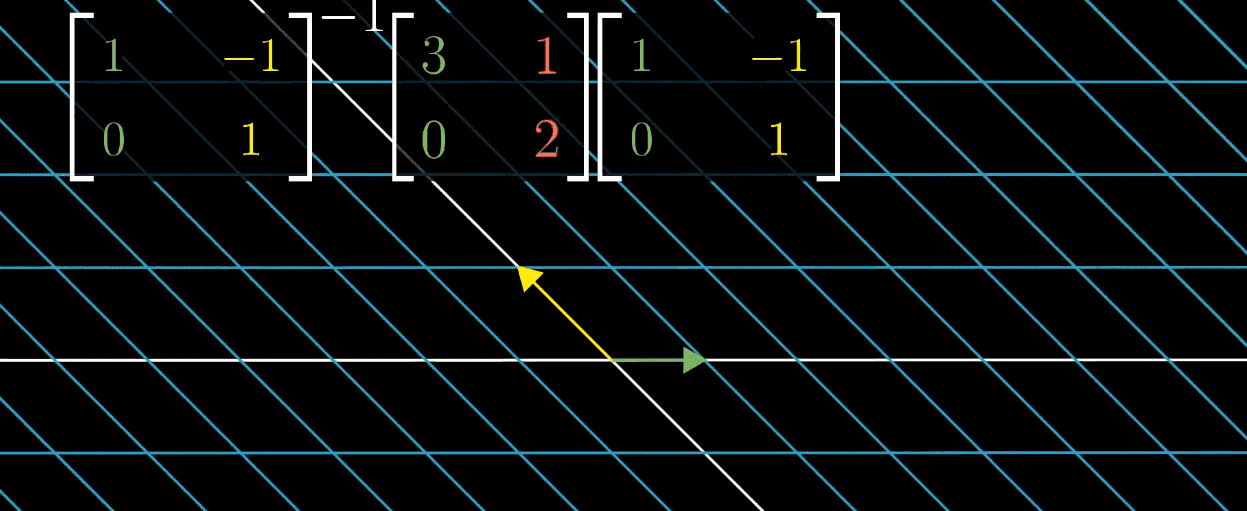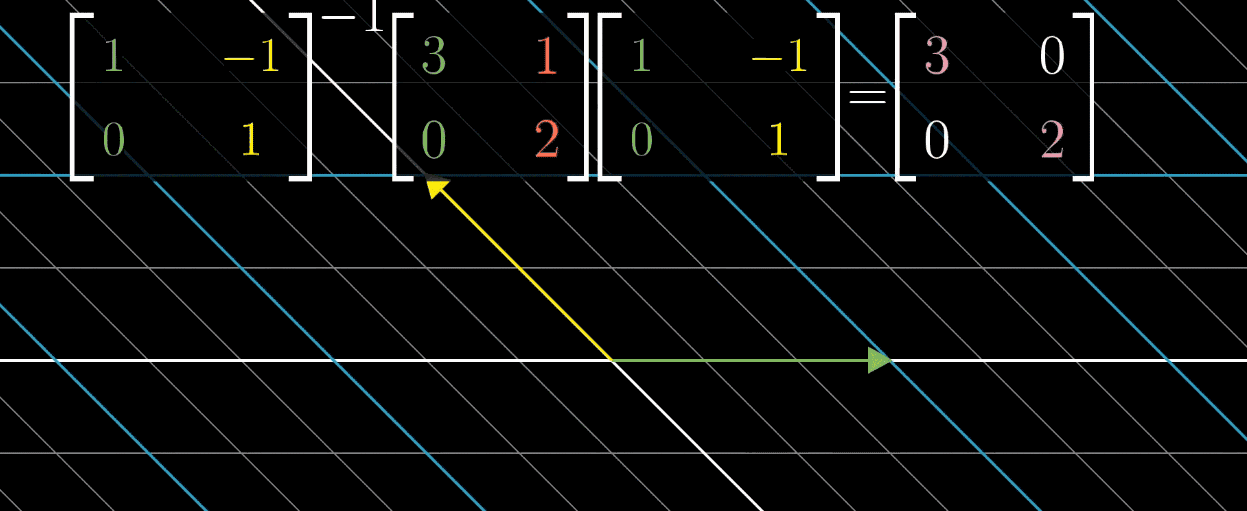
但需要说明的是,并不是所有的矩阵都能对角化,比如 Shear 变换,它的特征向量不够多,不足以张成一个空间
线性代数的一切概念,如行列式和特征向量,它们并不受所选坐标系的影响,但是这两者是暗含于空间中的性质
这里所说的空间是什么意思呢?
10. 抽象向量空间
10.1 函数与向量
从某种意义上来说,函数实际上也只是另一种向量,对于函数来说,也有可加性,可比性
你能发现,这两个性质和向量加法与向量乘法是息息相关的。所以我们对于矩阵中所有定义的概念和方法,都可以相对应的应用到函数中。如函数的线性变换:函数接受一个函数,并把它变成另一个函数。如微积分中可以找到一个形象的例子——导数。关于这一点,你听到的可能是【算子】,而不是【变换】,但他们所要表达的思想是一样的
以导数为例,既然两者是一个东西,那么我们可不可以使用矩阵来描述多项式空间呢?
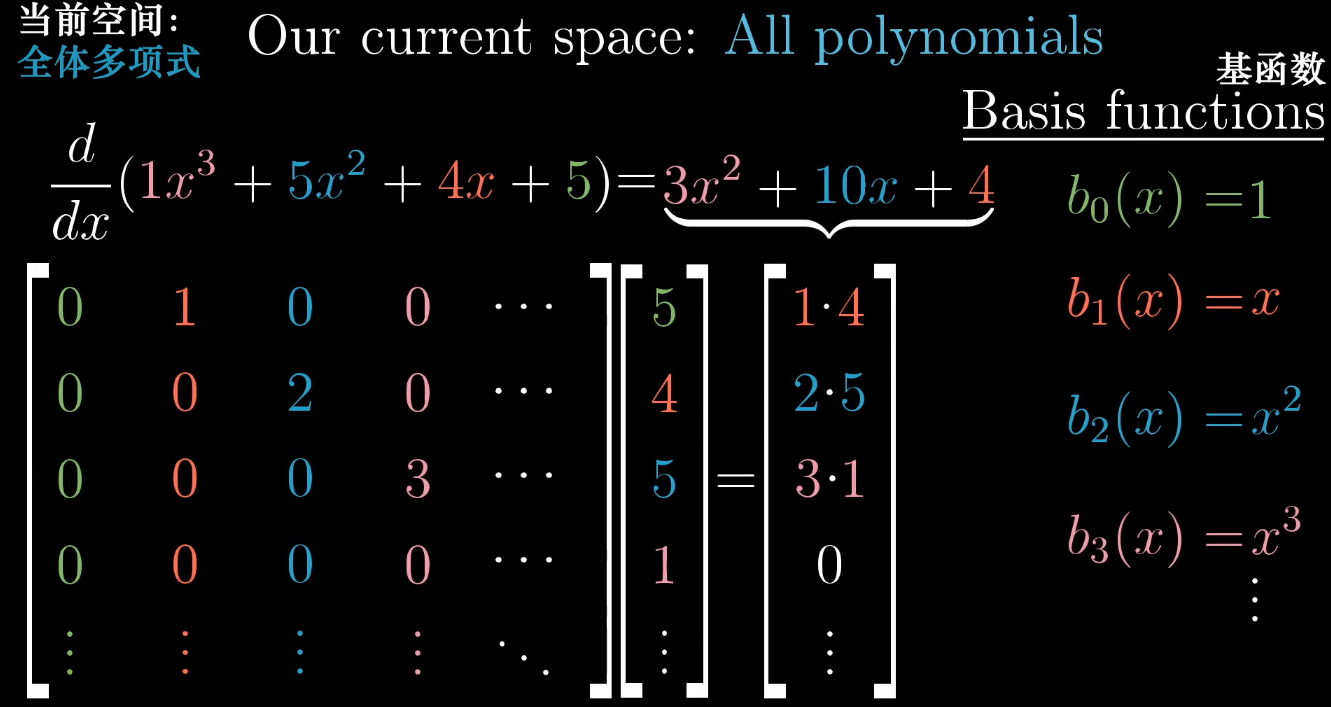
如上图,以取 $x$ 的不同幂次方作为基函数,然后既可以写出求导变换的矩阵。这更进一步佐证了开篇提到的关键句子,矩阵 = 变换的数字表达
| 线性代数 | 函数 |
|---|---|
| 线性变换 | 线性算子 |
| 点积 | 内积 |
| 特征向量 | 特征函数 |
如上表一样,相同的概念只是在不同的领域有着不同的名称罢了。
有很多类似向量的不同事物,只要你处理的对象具有合理的数乘和相加的概念,线性代数中所有关于向量,线性变换和其他的概念都应该使用与它。作为数学家,你可能希望你发现的规律不只对一个特殊情况适用,对其他类似向量的事物都有普适性
10.2 向量空间
这些类似向量的事物,比如箭头、一组数、函数等,他们构成的集合被称为:向量空间
向量加法和向量数乘的规则 - 被称为公理,如下图
![][img-34]
它仅仅是一个待查列表,以保证向量加法和数乘的概念确实是你所希望的那样。这些公理是一种媒介,用来连接数学家和所有想要把这些结论应用于新的向量空间的人
仅仅根据这些公理描述一个空间,而不是集中于某一个特定的向量上。简而言之,这就是为什么你阅读的每一本教科书都会根据可加性和成比例来定义线性变换
10.3 总结
对于【向量是什么】这个问题,数学家会直接忽略不作答。向量的形式并不重要,只要相加和数乘的概念遵守八条公理即可。就和问 “3” 究竟是什么一样。在数学中,他被看作是所有三个东西的集合的抽象概念,从而让你用一个概念就能推导出所有三个东西的集合。向量也是如此,它有很多种体现,但是数学把它抽象成【向量空间】这样一个无形(抽象)的概念
普适的代价是抽象(abstractness is the price of generality)。学习的过程只能来源于解决问题,来源于带有思考的不断重复,但如果你具备了正确的直观,你会再以后的学习中更加高效

